题目内容
13.已知一次函数y=kx+3经过点(2,1),则一次函数的图象经过的象限是( )| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第二、三、四象限 | D. | 第一、三、四象限 |
分析 将点的坐标代入到一次函数解析式中,求出k值即可得出一次函数解析式,结合k、b的值即可断定一次函数经过的象限.
解答 解:∵一次函数y=kx+3经过点(2,1),
∴1=2k+3,解得:k=-1.
∴一次函数的解析式为y=-x+3.
∵k=-1<0,b=3>0,
∴一次函数的图象经过的象限是:第一、二、四象限.
故选B.
点评 本题考查了待定系数法求函数解析式以及一次函数的图象,解题的关键是求出一次函数解析式.本题属于基础题,难度不大,解决该题型题目时,根据点的坐标结合待定系数法求出函数解析式,再根据解析式中的k、b值即可断定函数图象所过的象限.

练习册系列答案
相关题目
3.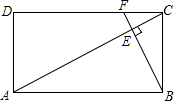 如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )
如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )
 如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )
如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )| A. | $\frac{1}{16}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{25}$ |
1.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.已知1微米相当于1米的一百万分之一,则2.5微米用科学记数可表示为( )
| A. | 2.5×10-7米 | B. | 2.5×10-6米 | C. | 2.5×107米 | D. | 2.5×106米 |
8. 如图,l1∥l2,∠3=30°,∠2=100°,则∠1=( )
如图,l1∥l2,∠3=30°,∠2=100°,则∠1=( )
 如图,l1∥l2,∠3=30°,∠2=100°,则∠1=( )
如图,l1∥l2,∠3=30°,∠2=100°,则∠1=( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
13.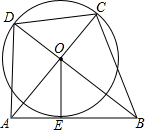 如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BD的延长线交⊙O于C、D.若⊙O的半径为1,则四边形ABCD面积最小值为( )
如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BD的延长线交⊙O于C、D.若⊙O的半径为1,则四边形ABCD面积最小值为( )
 如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BD的延长线交⊙O于C、D.若⊙O的半径为1,则四边形ABCD面积最小值为( )
如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BD的延长线交⊙O于C、D.若⊙O的半径为1,则四边形ABCD面积最小值为( )| A. | 2+3$\sqrt{2}$ | B. | $\frac{3+2\sqrt{2}}{2}$ | C. | 4+2$\sqrt{2}$ | D. | 3+3$\sqrt{2}$ |
14.下列运算正确的是( )
| A. | a2•a3=a6 | B. | ($\frac{1}{2}$)-1=-2 | C. | |-6|=6 | D. | $\sqrt{16}$=±4 |
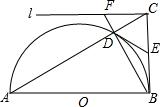 如图,△ABC中,∠ABC=90°,以AB为直径作半圆O,交斜边AC于点D,过点D作半圆O的切线DE,交BC于点E.
如图,△ABC中,∠ABC=90°,以AB为直径作半圆O,交斜边AC于点D,过点D作半圆O的切线DE,交BC于点E.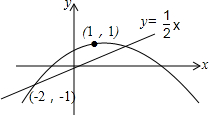 如图,二次函数y=ax2+bx+c的图象经过(-2,-1),(1,1)两点,下列判断:
如图,二次函数y=ax2+bx+c的图象经过(-2,-1),(1,1)两点,下列判断: