题目内容
16．当k的值为6或-2时，抛物线y=x2+kx+k+3与x轴只有一个公共点．分析 令y=0，则关于x的一元二次方程x2+kx+k+3=0的根的判别式△=0，据此列出关于k的新方程，通过解新方程即可求得k的值．
解答 解：令y=0，则当抛物线y=x2+kx+k+3与x轴只有一个公共点时，
关于x的一元二次方程x2+kx+k+3=0的根的判别式△=0，
即k2-4×1×（k+3）=0，
解得：k=6或k=-2．
故答案为：6或-2．
点评 本题考查了抛物线与x轴的交点以及根的判别式．运用“二次函数y=ax2+bx+c与x轴的交点个数与系数的关系：当b2-4ac=0时，只有一个交点”求解即可．
练习册系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
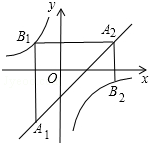如图，已知点A1，A2，…，An均在直线y=x-2上，点B1，B2，…，Bn均在双曲线y=-$\frac{4}{x}$上，并且满足：A1B1⊥x轴，B1A2⊥y轴，A2B2⊥x轴，B2A3⊥y轴，…，AnBn⊥x轴，BnAn+1⊥y轴，…，记点An的横坐标为an（n为正整数）．若a1=-2，则a2016=1．
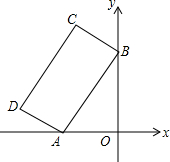如图，矩形ABCD的两个顶点A，B在坐标轴上，AD：AB=1：2，且A（-2，0），∠BAO=60°，反比例函数y=$\frac{k}{x}$（k≠0）的图象恰好经过该矩形的顶点，则k=-2-$\sqrt{3}$或-6-$\sqrt{3}$．
1．PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．已知1微米相当于1米的一百万分之一，则2.5微米用科学记数可表示为（ ）
| A． | 2.5×10-7米 | B． | 2.5×10-6米 | C． | 2.5×107米 | D． | 2.5×106米 |
8．
如图，l1∥l2，∠3=30°，∠2=100°，则∠1=（ ）
如图，l1∥l2，∠3=30°，∠2=100°，则∠1=（ ）| A． | 100° | B． | 110° | C． | 120° | D． | 130° |
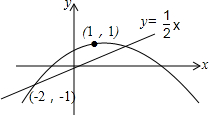如图，二次函数y=ax2+bx+c的图象经过（-2，-1），（1，1）两点，下列判断：