��Ŀ����
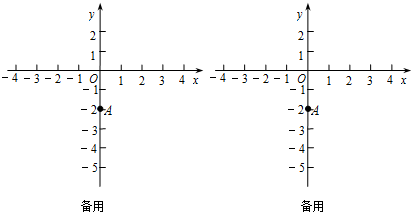
12����ͼ1����֪����ֽƬABCD�������²�����в��������ضԽ���AC��������ͼ2�����ڹ̶���ADC������ABC��2cm/s���ٶȣ�������CD�ķ����˶������˶�ʱ��Ϊts���˶��С�ABC�Ķ���A��B��C����Ӧ�ĵ�ֱ����A�䡢B�䡢C�䣬�ҵ�t=2ʱ��B�����ACD�Ķ���A�غϣ���1������ͼ3�����ó߹油ȫ��t=1ʱ��ͼ�Σ�������ͼ�ۼ�����д�����������������ѣ�������˱�ע��ĸ����
��2����������ƽ�ƹ����У���A��B��C�����ACD���ص����ֵ���������ֵΪ3��
����֤������t=1ʱ��A��B��C�����ACD���ص����ֵ����ȡ�����ֵ��
����ֱ��д����t=2ʱ�㣬A�����C֮��ľ���$\sqrt{73}$��
����̽������tΪ��ֵʱ��A��C��B��Dǡ�û��ഹֱ��
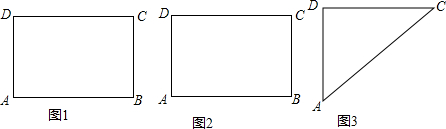
���� ��1��ֱ������ƽ�Ƶ����ʷֱ�ó���Ӧ��C�䣬B���λ�ã������ó�A���λ�ã�
��2����ֱ���������������ε��ж������ʵó���A��B��C�����ACD���ص����ֵ����������ϵʽ�������ó��𰸣�
�ڸ�����֪�������AD�ij����������ù��ɶ����ó��𰸣�
���������ε����ʽ�Ϲ��ɶ����ó��𰸣�
���  �⣺��1����ͼ1��ʾ��
�⣺��1����ͼ1��ʾ��
��2������ͼ1����B��C��=b��������֪��A��B��=AB=2��2=4��
��DA��B��C�䣬
���A��AE�ס�A��B��C�䣬
��$\frac{AE}{B��C��}$=$\frac{AA��}{A��B��}$��
$\frac{AE}{b}$=$\frac{2t}{4}$��
��AE=$\frac{bt}{2}$��
���A��B��C�����ACD���ص����ֵ������
S=$\frac{bt}{2}$��4-2t��=-b��t-1��2+b��
�൱t=1ʱ����A��B��C�����ACD���ص����ֵ����ȡ�����ֵ��
����ͼ1���ߡ�A��B��C�����ACD���ص����ֵ���������ֵΪ3��
��b=3��
�ߵ�t=1ʱ����A��B��C�����ACD���ص����ֵ����ȡ�����ֵ��
��AE��AB��=3��
��AE=AA��=AB��=2��
��AE=$\frac{3}{2}$��
��AD=3��
��ͼ2������A��C��
��A��C=$\sqrt{A��{B}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+{3}^{2}}$=$\sqrt{73}$��
�ʴ�Ϊ��$\sqrt{73}$��
��������֪��A��B���CD��A��B��=CD��
���ı���A��B��CD�����Σ�
����A��D����Rt��A��AD��AA��=2t��A��D=A��B��=4��AD=3��
�ɹ��ɶ����ã�2t��2+32=42��
��t=$\frac{\sqrt{7}}{2}$��
�൱t=$\frac{\sqrt{7}}{2}$ʱ��A��C��B��Dǡ�û��ഹֱ��
���� ������Ҫ�������ı����ۺ��Լ����ε����ʡ����ɶ��������������ε��ж������ʵ�֪ʶ����ȷ�ó�AD�ij��ǽ���ؼ���

 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�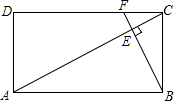 ��ͼ������ABCD�У�F��DC��һ�㣬BF��AC������ΪE��$\frac{AD}{AB}=\frac{1}{2}$����CEF�����ΪS1����AEB�����ΪS2����$\frac{{S}_{1}}{{S}_{2}}$��ֵ���ڣ�������
��ͼ������ABCD�У�F��DC��һ�㣬BF��AC������ΪE��$\frac{AD}{AB}=\frac{1}{2}$����CEF�����ΪS1����AEB�����ΪS2����$\frac{{S}_{1}}{{S}_{2}}$��ֵ���ڣ�������| A�� | $\frac{1}{16}$ | B�� | $\frac{1}{5}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{25}$ |
| A�� | y1��y2��y3 | B�� | y1��y3��y2 | C�� | y3��y1��y2 | D�� | y2��y3��y1 |
| A�� | 2.5��10-7�� | B�� | 2.5��10-6�� | C�� | 2.5��107�� | D�� | 2.5��106�� |
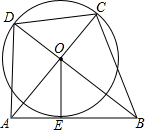 ��ͼ��Rt��AOB�У�OA��OB����O��AB�����ڵ�E��AO��BD���ӳ��߽���O��C��D������O�İ뾶Ϊ1�����ı���ABCD�����СֵΪ��������
��ͼ��Rt��AOB�У�OA��OB����O��AB�����ڵ�E��AO��BD���ӳ��߽���O��C��D������O�İ뾶Ϊ1�����ı���ABCD�����СֵΪ��������| A�� | 2+3$\sqrt{2}$ | B�� | $\frac{3+2\sqrt{2}}{2}$ | C�� | 4+2$\sqrt{2}$ | D�� | 3+3$\sqrt{2}$ |
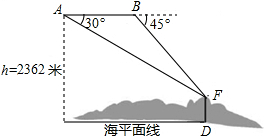 ���Һ���ֽ��й����㵺��߷�����Ϊ�����塱�����Ե��㵺���г�̬������Ѳ������ͼ����һ��Ѳ�������У�Ѳ���ɻ����и߶�Ϊ2362�ף��ڵ�A��ø��嶥F��ĸ���Ϊ30�㣬���ַ���ǰ��1464����B�����F�㸩��Ϊ45�㣬��ݴ˼�����㵺����ߺ��θ߶ȶ����ף�����������������ο���ֵ��$\sqrt{3}$=1.732��$\sqrt{2}$=1.414��
���Һ���ֽ��й����㵺��߷�����Ϊ�����塱�����Ե��㵺���г�̬������Ѳ������ͼ����һ��Ѳ�������У�Ѳ���ɻ����и߶�Ϊ2362�ף��ڵ�A��ø��嶥F��ĸ���Ϊ30�㣬���ַ���ǰ��1464����B�����F�㸩��Ϊ45�㣬��ݴ˼�����㵺����ߺ��θ߶ȶ����ף�����������������ο���ֵ��$\sqrt{3}$=1.732��$\sqrt{2}$=1.414��