题目内容
2.为了节约资源,科学指导居民改善居住条件,小王向房管部分提出了一个购买商品房的政策性方案.| 人均住房面积(平方米) | 单价(万元/平方米) |
| 不超过30平方米 | 0.6 |
| 超过30平方米不超过m平方米的部分(45≤m≤60) | 0.8 |
| 超过m平方米部分 | 1 |
(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;
(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式(m为常数);
(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元且102<y≤105时,求m的取值范围.
分析 (1)根据房款=房屋单价×人均住房面积就可以表示出应缴房款;
(2)由分段函数当0≤x≤30,当30<x≤m时,当x>m时,分别求出y与x之间的表达式即可;
(3)当50≤m≤60和当45≤m<50时,分别讨论建立不等式组就可以求出结论.
解答 解:(1)由题意,某三口之家的人均住房面积为:$\frac{120}{3}$=40(平方米)
得三口之家应缴纳房款为:0.6×3×30+0.8×3×10=78(万元);
(2)由题意,得
①当0≤x≤30时,y=0.6×3x=1.8x
②当30<x≤m时,y=1.8×30+0.8×3×(x-30)=2.4x-36,
③当x>m时,y=0.6×3×30+0.8×3(m-30)+1×3×(x-m)=3x-18-0.6m
∴y=$\left\{\begin{array}{l}{1.8x(0≤x≤30)}\\{2.4x-36(30<x≤m)(45≤x≤60)}\\{3x-18-0.6m(x>m)}\end{array}\right.$
(3)由题意,得
①当50≤m≤60时,y=2.4×50-18=102(舍).
②当45≤m<50时,y=3×50-0.6m-18=132-0.6m.
∵102<y≤105,
∴102<132-0.6m≤105,
∴45≤m<50.
综合①②得45≤m<50.
点评 本题考查了房款=房屋单价×购房面积在实际生活中的运用,求分段函数的解析式的运用,建立不等式组求解的运用,解答本题时求出函数的解析式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.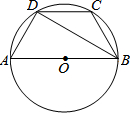 如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )
如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )
 如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )
如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=6cm,∠ABD=30°,则⊙O的面积为( )| A. | 25πcm2 | B. | 49πcm2 | C. | 32πcm2 | D. | 36πcm2 |
11.一个角的补角与这个角的余角的和比平角少10°,这个角为( )
| A. | 50 | B. | 60 | C. | 90 | D. | 120 |
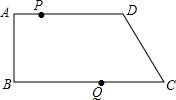 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=16cm,BC=22cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=16cm,BC=22cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒.