题目内容
12.(1)计算:(π-$\sqrt{3}$)0-($\frac{1}{2}$)-1-2cos60°(2)解分式方程:$\frac{2}{x+3}$=$\frac{1}{x-1}$.
分析 (1)首先根据零指数幂、负整数指数幂的运算方法,求出(π-$\sqrt{3}$)0、($\frac{1}{2}$)-1的值各是多少;然后求出2cos60°的值,再从左向右依次计算即可.
(2)根据分式方程的解法解答即可,注意检验.
解答 解:(1)(π-$\sqrt{3}$)0-($\frac{1}{2}$)-1-2cos60°
=1-2$-2×\frac{1}{2}$
=-1-1
=-2
(2)∵$\frac{2}{x+3}$=$\frac{1}{x-1}$,
∴2(x-1)=x+3,
解得x=5,
把x=5代入原方程,可得
左边=$\frac{2}{5+3}=\frac{1}{4}$,右边=$\frac{1}{5-1}=\frac{1}{4}$,
∵左边=右边,
∴x=5是方程$\frac{2}{x+3}$=$\frac{1}{x-1}$的解.
点评 (1)此题主要考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:(1)a0=1(a≠0);(2)00≠1.
(2)此题还考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.
(3)此题还考查了分式方程的解法,要熟练掌握解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.
(4)此题还考查了特殊角的三角函数值,要熟练掌握.

练习册系列答案
相关题目
2.为了节约资源,科学指导居民改善居住条件,小王向房管部分提出了一个购买商品房的政策性方案.
根据这个购房方案:
(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;
(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式(m为常数);
(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元且102<y≤105时,求m的取值范围.
| 人均住房面积(平方米) | 单价(万元/平方米) |
| 不超过30平方米 | 0.6 |
| 超过30平方米不超过m平方米的部分(45≤m≤60) | 0.8 |
| 超过m平方米部分 | 1 |
(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;
(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式(m为常数);
(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元且102<y≤105时,求m的取值范围.
 如图,反比例函数y=$\frac{k}{x}$的图象过面积为$\sqrt{2}$的矩形ABOC的顶点A,则k=-$\sqrt{2}$.
如图,反比例函数y=$\frac{k}{x}$的图象过面积为$\sqrt{2}$的矩形ABOC的顶点A,则k=-$\sqrt{2}$.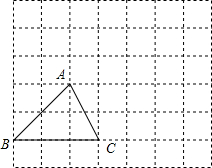 △ABC在网格中如图所示,请根据下列提示作图:
△ABC在网格中如图所示,请根据下列提示作图: