题目内容
12．已知正多边形每个内角与它的外角的差为90°，求这个多边形内角的度数和边数．分析 一个多边形的每个内角都相等，每个内角都比外角大90°，又由于内角与外角的和是180度．设外角是x，则内角是180°-x，列方程求解即可．
解答 解：设外角是x，则内角是180°-x，依题意有
180°-x=x+90°，
解得x=45°，
180°-x=135°，
而任何多边形的外角是360°，
则多边形中外角的个数是360÷45=8，
故这个多边形的边数是8，每个内角的度数是135°．
点评 本题考查了多边形内角与外角，根据多边形的内角与外角的关系转化为方程的问题，并利用了多边形的外角和定理；已知外角求边数的这种方法是需要熟记的内容．
练习册系列答案
相关题目
2．为了节约资源，科学指导居民改善居住条件，小王向房管部分提出了一个购买商品房的政策性方案．
根据这个购房方案：
（1）若某三口之家欲购买120平方米的商品房，求其应缴纳的房款；
（2）设该家庭购买商品房的人均面积为x平方米，缴纳房款y万元，请求出y关于x的函数关系式（m为常数）；
（3）若该家庭购买商品房的人均面积为50平方米，缴纳房款为y万元且102＜y≤105时，求m的取值范围．
| 人均住房面积（平方米） | 单价（万元/平方米） |
| 不超过30平方米 | 0.6 |
| 超过30平方米不超过m平方米的部分（45≤m≤60） | 0.8 |
| 超过m平方米部分 | 1 |
（1）若某三口之家欲购买120平方米的商品房，求其应缴纳的房款；
（2）设该家庭购买商品房的人均面积为x平方米，缴纳房款y万元，请求出y关于x的函数关系式（m为常数）；
（3）若该家庭购买商品房的人均面积为50平方米，缴纳房款为y万元且102＜y≤105时，求m的取值范围．
20．4的平方根是（ ）
| A． | 2 | B． | ±2 | C． | -2 | D． | 4 |
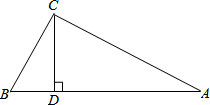如图所示，已知△ABC中，CD⊥AB于D，AC=4，BC=3，DB=$\frac{9}{5}$．