��Ŀ����
17��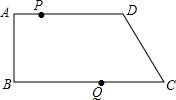 ��ͼ�����ı���ABCD�У�AD��BC����B=90�㣬AB=8cm��AD=16cm��BC=22cm����P�ӵ�A��������1cm/s���ٶ����D�˶�����Q�ӵ�Cͬʱ��������3cm/s���ٶ����B�˶�������һ�����㵽��˵�ʱ����һ������Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮
��ͼ�����ı���ABCD�У�AD��BC����B=90�㣬AB=8cm��AD=16cm��BC=22cm����P�ӵ�A��������1cm/s���ٶ����D�˶�����Q�ӵ�Cͬʱ��������3cm/s���ٶ����B�˶�������һ�����㵽��˵�ʱ����һ������Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮��1����tΪ����ʱ���ı���ABQP��Ϊ���Σ�
��2���ı���PBQD�Ƿ��ܳ�Ϊ���Σ����ܣ����t��ֵ�������ܣ���˵�����ɣ���̽����θı�Q����ٶȣ������˶�����ʹ�ı���PBQD��ijһʱ��Ϊ���Σ����Q���ٶȣ�
���� ��1����Ϊ��B=90�㣬AP��BQ���ɾ��ε��ж���֪��AP=BQʱ���ı���ABQP��Ϊ���Σ�
��2����ΪPD��BQ����PD=BQ=BPʱ���ı���PBQD�ܳ�Ϊ���Σ�����PD=BQ����˶�ʱ��t��ֵ���ٴ�����BP������BP��PD���жϴ�ʱ�ı���PBQD���ܳ�Ϊ���Σ���Q����ٶȸı�Ϊvcm/sʱ���ı���PBQD��ʱ��tΪ���Σ�����PD=BQ=BP�г�����v��t�ķ����飬�ⷽ���鼴�������Q���ٶȣ�
��� �⣺��1���ߡ�B=90�㣬AP��BQ��
�൱AP=BQʱ���ı���ABQP��Ϊ���Σ�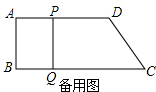
��ʱ��t=22-3t�����t=$\frac{11}{2}$��
�൱t=$\frac{11}{2}$sʱ���ı���ABQP��Ϊ���Σ�
��2��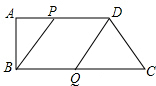 �ı���PBQD���ܳ�Ϊ���Σ��������£�
�ı���PBQD���ܳ�Ϊ���Σ��������£�
��PD��BQ��
�൱PD=BQ=BPʱ���ı���PBQD�ܳ�Ϊ���Σ�
��PD=BQ����16-t=22-3t�����t=3��
��t=3ʱ��PD=BQ=13��BP=$\sqrt{A{B}^{2}+A{P}^{2}}$=$\sqrt{{8}^{2}+{t}^{2}}$=$\sqrt{{8}^{2}+{3}^{2}}$=$\sqrt{73}$��13��
���ı���PBQD���ܳ�Ϊ���Σ�
���Q����ٶȸı�Ϊvcm/sʱ���ܹ�ʹ�ı���PBQD��ʱ��tsΪ���Σ�
�����⣬��$\left\{\begin{array}{l}{16-t=22-vt}\\{16-t=\sqrt{{8}^{2}+{t}^{2}}}\end{array}\right.$�����$\left\{\begin{array}{l}{t=6}\\{v=2}\end{array}\right.$��
�ʵ�Q���ٶ�Ϊ2cm/sʱ���ܹ�ʹ�ı���PBQD��ijһʱ��Ϊ���Σ�
���� �������������Ҫ�����˾��Ρ����ε��ж������ɶ������������ε��ж������ʣ��Լ����̺ͷ������ڼ���ͼ���е�Ӧ�ã��Ѷ����У��ú�t�Ĵ���ʽ��ȷ��ʾ������߶εij����ǽ���Ĺؼ���

 С�����ϵ�д�
С�����ϵ�д�| A�� | 130�� | B�� | 50�� | C�� | 100�� | D�� | ����ȷ�� |
| �˾�ס�������ƽ���ף� | ���ۣ���Ԫ/ƽ���ף� |
| ������30ƽ���� | 0.6 |
| ����30ƽ���ײ�����mƽ���IJ��֣�45��m��60�� | 0.8 |
| ����mƽ���ײ��� | 1 |
��1����ij����֮��������120ƽ������Ʒ��������Ӧ���ɵķ��
��2����ü�ͥ������Ʒ�����˾����Ϊxƽ���ף����ɷ���y��Ԫ�������y����x�ĺ�����ϵʽ��mΪ��������
��3�����ü�ͥ������Ʒ�����˾����Ϊ50ƽ���ף����ɷ���Ϊy��Ԫ��102��y��105ʱ����m��ȡֵ��Χ��