题目内容
15.化简$\frac{x-y}{\sqrt{x}-\sqrt{y}}$-$\sqrt{x+y-2\sqrt{xy}}$,对此题有位同学作如下解答:解:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$-$\sqrt{x+y-2\sqrt{xy}}$=$\frac{(x-y)(\sqrt{x}-\sqrt{y})}{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}$-$\sqrt{(\sqrt{x}-\sqrt{y})^{2}}$=$\frac{(x-y)(\sqrt{x}-\sqrt{y})}{x-y}$-($\sqrt{x}$-$\sqrt{y}$)=$\sqrt{x}$-$\sqrt{y}$-$\sqrt{x}$+$\sqrt{y}$=0.位同学的解答正确吗?若不正确,请指出错误原因,并加以改正.
分析 根据题目中的步骤即可发现问题所在,分类讨论x与y的大小,然后根据分母有理化即可解答本题.
解答 解:该同学解答不正确,
错误原因是不知道x与y哪个大,从而x-y是正值还是负值不清楚,故解答错误,并且第一步的式子就抄错了,
改正:当x=y时,
$\frac{x-y}{\sqrt{x}-\sqrt{y}}$-$\sqrt{x+y-2\sqrt{xy}}$无意义;
当x>y时,
$\frac{x-y}{\sqrt{x}-\sqrt{y}}$-$\sqrt{x+y-2\sqrt{xy}}$=$\frac{(\sqrt{x}-\sqrt{y})(\sqrt{x}+\sqrt{y})}{\sqrt{x}-\sqrt{y}}-\sqrt{(\sqrt{y}-\sqrt{x})^{2}}$=$(\sqrt{x}+\sqrt{y})-(\sqrt{x}-\sqrt{y})$=$\sqrt{x}+\sqrt{y}-\sqrt{x}+\sqrt{y}$=2$\sqrt{y}$;
当x<y时,
$\frac{x-y}{\sqrt{x}-\sqrt{y}}$-$\sqrt{x+y-2\sqrt{xy}}$=$\frac{(\sqrt{x}-\sqrt{y})(\sqrt{x}+\sqrt{y})}{\sqrt{x}-\sqrt{y}}-\sqrt{(\sqrt{y}-\sqrt{x})^{2}}$=$(\sqrt{x}+\sqrt{y})-(\sqrt{y}-\sqrt{x})$=$\sqrt{x}+\sqrt{y}-\sqrt{y}+\sqrt{x}$=2$\sqrt{x}$
点评 本题考查二次根式的混合运算,解答本题的关键是明确二次根式混合运算的计算方法.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目

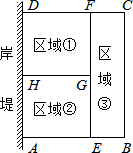 为了节省材料,某水产养殖户利用水库的岸堤(岸堤长15m)为一边,用总长为80m的栅栏围在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为y m2.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤长15m)为一边,用总长为80m的栅栏围在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为y m2. 如图,Rt△ABC中,AB=10,BC=6,E是AC上一点,AE=5,ED⊥AB,垂足为D,则AD的长为4.
如图,Rt△ABC中,AB=10,BC=6,E是AC上一点,AE=5,ED⊥AB,垂足为D,则AD的长为4. 如图,用小立方块搭成一个几何体,使得它的从正面与上面看到的图形如图所示.他至少需要10个小立方块,最多需要13个小立方块.
如图,用小立方块搭成一个几何体,使得它的从正面与上面看到的图形如图所示.他至少需要10个小立方块,最多需要13个小立方块.