题目内容
10.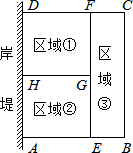 为了节省材料,某水产养殖户利用水库的岸堤(岸堤长15m)为一边,用总长为80m的栅栏围在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为y m2.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤长15m)为一边,用总长为80m的栅栏围在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为y m2.(1)用含x的代数式表示BE的长:BE=-$\frac{1}{4}$x+10;
(2)求y与x之间的函数关系式,并注明自变量x的取值范围;
(3)求x为何值时,y有最大值,最大值是多少.
分析 (1)根据三个矩形面积相等,得到矩形AEFD面积是矩形BCFE面积的2倍,可得出AE=2BE,设BE=a,则有AE=2a,根据围栏的总长为80m表示出a;
(2)表示出AB的长,进而根据矩形的面积公式表示出y与x的关系式,并求出x的范围即可;
(2)利用二次函数的性质求出y的最大值,以及此时x的值即可.
解答 解:(1)∵三块矩形区域的面积相等,
∴矩形AEFD面积是矩形BCFE面积的2倍,
∴AE=2BE,
设BE=FC=a,则AE=HG=DF=2a,
∴DF+FC+HG+AE+EB+EF+BC=80,即8a+2x=80,
∴a=-$\frac{1}{4}$x+10,即BE=-$\frac{1}{4}$x+10,
故答案为:-$\frac{1}{4}$x+10;
(2)由(1)知3a=-$\frac{3}{4}$x+30,
∴y=(-$\frac{3}{4}$x+30)x=-$\frac{3}{4}$x2+30x,
∵a=-$\frac{1}{4}$x+10>0,
∴15≤x<40,
则y=-$\frac{3}{4}$x2+30x(15≤x<40);
(3)∵y=-$\frac{3}{4}$x2+30x=-$\frac{3}{4}$(x-20)2+300(0<x<40),且二次项系数为-$\frac{3}{4}$<0,
∴当x=20时,y有最大值,最大值为300平方米.
点评 此题考查了二次函数的应用以及列代数式,根据题意表示出矩形的宽并熟练掌握二次函数的性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
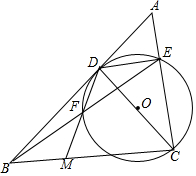 如图,在△ABC中,∠ACB=90°,点D在AB上,以CD为直径的⊙O交AC于点E,连接BE交⊙O于点F,延长DF交BC于点M,且∠BDF=∠DEB.
如图,在△ABC中,∠ACB=90°,点D在AB上,以CD为直径的⊙O交AC于点E,连接BE交⊙O于点F,延长DF交BC于点M,且∠BDF=∠DEB.
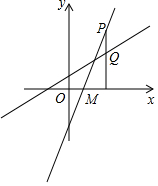 如图,点P是一次函数y=3x-2图象上的动点,过点P作直线PM⊥Ox,垂足为点M,PM交一次函数y=$\frac{2}{3}$x+1的图象于点Q,设点P的横坐标为m,当线段PQ=1时,m的值为$\frac{12}{7}$.
如图,点P是一次函数y=3x-2图象上的动点,过点P作直线PM⊥Ox,垂足为点M,PM交一次函数y=$\frac{2}{3}$x+1的图象于点Q,设点P的横坐标为m,当线段PQ=1时,m的值为$\frac{12}{7}$.