题目内容
3.阅读材料:在一次数学活动课上,老师出了一道题:
(1)解方程x2-3x-4=0.
巡视后,老师发现同学们解此题的方法有公式法、配方法和十字相乘法(分解因式法).接着,老师请大家用自己熟悉的方法解第二题:
(2)解关于x的方程mx2+(m-4)x-4=0(m为非零常数).
老师继续巡视,及时观察、点拨大家.再接着,老师将第二道题变为第三道题:
(3)已知关于x的函数y=mx2+(m-4)x-4(m为非零常数).求证:不论m为何值,此函数的图象恒过两个定点.
老师发现小明第(3)题的解法新颖,小明的解法如下:
∵y=mx2+(m-4)x-4
∴(x2+x)m-4x-4-y=0
∵上式对任何非零实数m都成立,所以
$\left\{\begin{array}{l}{{x}^{2}+x=0}\\{-4x-4-y=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=0}\\{y=-4}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$
∴此函数的图象恒过两个定点(-1,0)和(0,-4).
表扬了小明后,老师给出第四道题:
(4)已知关于x的函数y=mx2+(4m-3)x+4m-2(m为非零常数).求证:不论m为何值,此函数的图象恒过定点.
请你用自己熟悉的方法完成第(1)题和第(2)题,用小明的方法完成第(4)题.
分析 (1)用因式分解法解即可.
(2)用十字相乘法(分解因式法)即可解决.
(4)模仿(3)把问题转化为方程组解决.
解答 解:(1)∵x2-3x-4=0,
∴(x-4)(x+1)=0,
∴x=4或-1;
(2)∵mx2+(m-4)x-4=0(m≠0),
∴(x+1)(mx-4)=0,
∴x=-1或$\frac{4}{m}$;
(4)∵y=mx2+(4m-3)x+4m-2,
∴y=mx2+4mx-3x+4m-2,
∴(x2+4x+4)m-y-3x-2=0,
∵$\left\{\begin{array}{l}{{x}^{2}+4x+4=0}\\{-y-3x-2=0}\end{array}\right.$,
交点$\left\{\begin{array}{l}{x=-2}\\{y=4}\end{array}\right.$,
∴此函数的图象恒过定点(-2,4)
点评 本题考查二次函数图象上点的特征、二次函数过定点问题、一元二次方程的解法等知识,解题的关键是理解题意,学会模仿,学会把问题转化为方程组解决,属于中考常考题型.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
11.小明原有63元,如图记录了他今天所有支出,其中饮料支出的金额被涂黑.若每瓶饮料的售价为5元,则小明可能剩下的钱数为3、8或13元.
| 支出 | 金额(元) |
| 早餐 | 10 |
| 午餐 | 15 |
| 晚餐 | 20 |
| 饮料 | ■ |
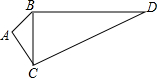 如图,已知AB=$\sqrt{3}$,AC=2,AB⊥AC,BD=3,CD=4.
如图,已知AB=$\sqrt{3}$,AC=2,AB⊥AC,BD=3,CD=4.