Question

7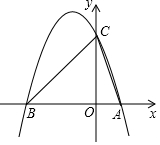．如图，在平面直角坐标系中，y=ax²+bx+c（a＜0）与x轴交于点A（x₁，0），B（x₂，0）两点（x₂＜0＜x₁），与y轴正半轴交于点C．已知OA：OB=1：3，OB=OC，△ABC的面积S_△ABC=6．
（1）求经过A、B、C三点的抛物线的函数表达式；
（2）设E是y轴左侧抛物线上异于点B的一个动点，过点E作x轴的平行线交抛物线于另一点F，过点F作FG垂直于x轴于点G，再过点E作EH垂直于x轴于点H，得到矩形EFGH．则在点E的运动过程中，当矩形EFGH为正方形时，求出该正方形的边长；
（3）在抛物线上是否存在异于B、C的点M，使△MBC中BC边上的高为2$\sqrt{2}$？若存在，求出点M的坐标；若不存在，请说明理由．

Answer 1

分析 （1）设OA=x，则OB=OC=3x，依据三角形的面积公式可求得x=1，则A（1，0），B（-3，0），C（0，3），设抛物线的解析式为y=a（x+3）（x-1），将C（0，3）代入求得a的值即可；
（2）当点E在x轴的上方时．设E（x，-x²-2x+3）依据抛物线的对称性可求得F（-2-x，-x²-2x+3），然后用含x的式子可表示出EH和EF的长，然后依据EF=EH列方程求解即可；当点E在x轴的下方时，EH=|-x²-2x+3|=x²+2x-3．然后由EH=EF列方程求解即可；
（3）当点M在BC的下方时．过点M作直线MD∥BC，交y轴与D，过点D作DE⊥BC，垂足为E．先证明△DCE为等腰直角三角形，然后求得DC的长，从而得到点D的坐标，故此可得到MD的解析式，然后求得直线MD与抛物线的交点坐标即可；当点M在BC的上方时，同理可知CD=4，然后求得直线MD与抛物线的交点坐标即可．

解答 解：（1）设OA=x，则OB=OC=3x．
∵S_△ABC=6，
∴$\frac{1}{2}$AB•OC=6，即$\frac{1}{2}$×4x×3x=6，解得x=1．
∴A（1，0），B（-3，0），C（0，3）．
设抛物线的解析式为y=a（x+3）（x-1），将C（0，3），代入得：-3a=3，解得a=-1．
∴抛物线的解析式为y=-x²-2x+3．
（2）如图1所示：当点E在x轴的上方时．

设E（x，-x²-2x+3）．
∵抛物线的对称轴x=-$\frac{b}{2a}$=-1，E（x，-x²-2x+3），
∴F（-2-x，-x²-2x+3）．
∴EF=-2-2x．
∵四边形EFGH为正方形，
∴EH=EF，即-x²-2x+3=-2-2x，解得：x₁=-$\sqrt{5}$，x₂=$\sqrt{5}$（舍去）．
当点E在x轴的下方时，EH=|-x²-2x+3|=x²+2x-3．
由EH=EF得：x²+2x-3=-2-2x，解得：x=-2-$\sqrt{5}$或x=-2+$\sqrt{5}$（舍去）．
当x=-$\sqrt{5}$时，EF=-2-2×（-$\sqrt{5}$）=2$\sqrt{5}$-2．
当x=-2-$\sqrt{5}$时，EF=-2-2×（-2-$\sqrt{5}$）=2$\sqrt{5}$+2．
∴正方形的边长为2$\sqrt{5}$-2或2$\sqrt{5}$+2．
（3）如图2所示：当点M在BC的下方时，过点M作直线MD∥BC，交y轴与D，过点D作DE⊥BC，垂足为E．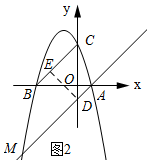

由平移的性质可知BC∥MD．
∵OC=OB，∠BOC=90°，
∴∠BCO=45°．
又∵∠DEC=90°，
∴CD=$\sqrt{2}$DE=$\sqrt{2}$×2$\sqrt{2}$=4．
∴D（0，-1）．
∴直线DM的解析式为y=x-1．
将y=x-1与y=-x²-2x+3联立，解得：x=1或x=-4，
∴点M的坐标为（-4，-5）或（1，0）．
当点M在BC的上方时，同理可知CD=4，
∴点D的坐标为（0，7），
∴直线MD的解析式为y=x+7．
将y=x+7与y=-x²-2x+3联立，方程组无解．
综上所述点M的坐标为（-4，-5）或（1，0）．

点评 本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求二次函数的解析式，三角形的面积公式，正方形的性质等知识，用含x的式子表示出EF和EH的长度是解答问题（2）的关键；求得点D的坐标是解答问题（3）的关键．