题目内容
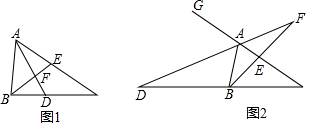
15.已知,点E是△ABC的边AC上的一点,∠AEB=∠ABC.请在下面的A,B两题中任选一题作答,我选择.A.如图1,若AD平分∠BAC,交BC于点D,交BE于点F.求证:∠EFD=∠ADC;
B.如图2,若AD平分△ABC的外角∠BAG,交边CB的延长线于点D,交BE的延长线于点F,判断∠F与∠D的数量关系,并说明理由.
分析 A、根据角平分线的定义得到∠BAD=∠CAD,由三角形的外角的性质得到∠EFD=∠CAD+∠AEB,∠ADC=∠ABC+∠DAC,于是得到结论;
B、根据角平分线的性质得到∠1=∠2,∵由对顶角的性质得到∠1=∠3,等量代换得到∠2=∠3,根据三角形的外角的性质即可得到结论.
解答 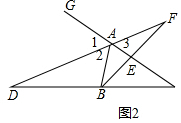 证明:∵AD平分∠BAC,
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵∠EFD=∠CAD+∠AEB,∠ADC=∠ABC+∠DAC,
∵∠AEB=∠ABC,
∴∠EFD=∠ADC;
B、∠F=∠D,
证明:∵AD平分△ABC的外角∠BAG,
∴∠1=∠2,∵1=∠3,
∴∠2=∠3,
∵∠AEB=∠F+∠3,∠ABC=∠D+∠2,∵∠ABC=∠AEB,∴∠F+∠3=∠D+∠2,
∴∠F=∠D.
点评 本题考查了三角形的角平分线的定义,三角形的外角的性质,熟练掌握三角形的外角的性质是解题的关键.

练习册系列答案
相关题目
6.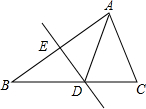 如图所示.将△ABC沿直线DE折叠后,使点B与点A重合,已知AC=4cm,△ADC的周长为11cm,则BC的长为( )
如图所示.将△ABC沿直线DE折叠后,使点B与点A重合,已知AC=4cm,△ADC的周长为11cm,则BC的长为( )
 如图所示.将△ABC沿直线DE折叠后,使点B与点A重合,已知AC=4cm,△ADC的周长为11cm,则BC的长为( )
如图所示.将△ABC沿直线DE折叠后,使点B与点A重合,已知AC=4cm,△ADC的周长为11cm,则BC的长为( )| A. | 11cm | B. | 15cm | C. | 7cm | D. | 10cm |
20.若三角形的两边长分别是4和6,第三边的长是一元二次方程x2-7x+12=0的一个实数根,则该三角形的周长是( )
| A. | 13 | B. | 14 | C. | 17 | D. | 13或14 |
5.下列计算,正确的是( )
| A. | -a2b+2a2b=a2b | B. | 3a-a=a | C. | 2a3+3a2=5a5 | D. | 3a+2a=5a2 |
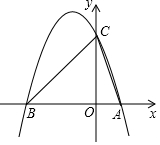 如图,在平面直角坐标系中,y=ax2+bx+c(a<0)与x轴交于点A(x1,0),B(x2,0)两点(x2<0<x1),与y轴正半轴交于点C.已知OA:OB=1:3,OB=OC,△ABC的面积S△ABC=6.
如图,在平面直角坐标系中,y=ax2+bx+c(a<0)与x轴交于点A(x1,0),B(x2,0)两点(x2<0<x1),与y轴正半轴交于点C.已知OA:OB=1:3,OB=OC,△ABC的面积S△ABC=6.