题目内容
9.预备知识:(1)线段中点坐标公式:在平面直角坐标系中,已知A(x1,y1),B(x2,y2),设点M为线段AB的中点,则点M的坐标为($\frac{{x}_{1}{+x}_{2}}{2}$,$\frac{{y}_{1}{+y}_{2}}{2}$).①设A(1,2),B(5,0),点M为线段AB的中点,则点M的坐标为(3,1).
②设线段CD的中点为点N,其坐标为(3,2),若端点C的坐标为(7,3),则端点D的坐标为(-1,-1).
(2)如图1,四边形ABCD中,AD∥BC,点E为DC的中点,连结AE并延长交BC的延长线于点F.求证:S四边形ABCD=S△ABF.(S表示面积)
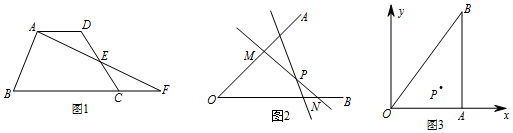
问题探究:如图2,在已知锐角∠AOB内有一定点P,过点P任意作一条直MN,分别交射线OA,OB于点M、N将直线MN绕着点P旋转的过程中发现,△MON的面积存在最小值,请问当直线MN在什么位置时,△MON的面积最小,并说明理由.
结论应用:如图3,在平面直角坐标系xoy中,已知点A在x轴上,点B在第一象限,且OA=3、AB=4、OB=5,若点P的坐标为(2,1),过点P的直线l分别交OB、AB于点M、N,求三角形BMN面积的最小值.
分析 预备知识:(1)根据线段的中点坐标公式即可得到结论;
(2)根据可以求得△ADE≌△FCE,就可以得出S△ADE=S△FCE就可以得出结论;
问题探究:根据问题情境的结论可以得出当直线旋转到点P是MN的中点时S△MON最小,过点M作MG∥OB交EF于G.由全等三角形的性质可以得出结论;
结论应用:如图3,由问题探究当点P是MN的中点时S△MBN最小,根据勾股定理的逆定理得到∠OAB=90°,求得AB⊥x轴,得到N点的横坐标为3,设M(a,b),根据线段的中点坐标公式得到a=1,过M作MC⊥OA于C,根据相似三角形的性质得到CM=$\frac{4}{3}$,得到AN=$\frac{2}{3}$,于是得到结论.
解答 解:预备知识:(1)①∵A(1,2),B(5,0),点M为线段AB的中点,
∴M($\frac{1+5}{2}$,$\frac{2+0}{2}$),即M(3,1),
故答案为:(3,1);
②设D(x,y),
由中点坐标公式得:$\frac{7+x}{2}$=3,$\frac{3+y}{2}$=2,
∴x=-1,y=-1,
∴D(-1,-1);
故答案为:(-1,-1);
(2)证明:∵AD∥BC,
∴∠ADE=∠FCE,
在△ADE与△FCE中,$\left\{\begin{array}{l}{∠ADE=FCE}\\{DE=CE}\\{∠AED=∠FEC}\end{array}\right.$,
∴△ADE≌△FCE,
∴S△ADE=S△FCE,
∴S四边形ABCD=S四边形ABCE+S△ADE=S四边形ABCE+S△FCE=S△ABF;
问题探究:
当直线旋转到点P是MN的中点时S△MON最小,
如图2,过点P的另一条直线EF交OA、OB于点E、F,设PF<PE,过点M作MG∥OB交EF于G,
由预备知识(2)可以得出当P是MN的中点时S四边形MOFG=S△MON.
∵S四边形MOFG<S△EOF,
∴S△MON<S△EOF,
∴当点P是MN的中点时S△MON最小;
结论应用:如图3,由问题探究当点P是MN的中点时S△MBN最小,
∵OA=3、AB=4、OB=5,
∴OA2+AB2=OB2,
∴∠OAB=90°,
∴AB⊥x轴,
∴N点的横坐标为3,
设M(a,b),
∵点P的坐标为(2,1),
∴$\frac{a+3}{2}$=2,
∴a=1,
过M作MC⊥OA于C,
∴OC=1,
∴MC∥AB,
∴△OCM∽△OAB,
∴$\frac{CM}{AB}=\frac{OC}{OA}$,即$\frac{CM}{4}=\frac{1}{3}$,
∴CM=$\frac{4}{3}$,
∵$\frac{CM+AN}{2}$=$\frac{2}{3}$,
∴AN=$\frac{2}{3}$,
∴S△MBN=S四边形ABMC-S四边形ANMC=$\frac{1}{2}$($\frac{4}{3}$+4)×(3-1)-$\frac{1}{2}$×($\frac{2}{3}$+$\frac{4}{3}$)×(3-1)=$\frac{10}{3}$,
∴三角形BMN面积的最小值是$\frac{10}{3}$.
点评 此题是几何变换综合题,主要考查了由特殊到一般的数学思想的运用,全等三角形的判定及性质的运用,勾股定理的逆定理的运用,四边形的面积公式的运用,三角形的面积公式的运用,解答时建立数学模型解答是关键.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案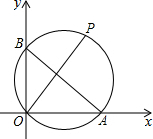 如图,点A的坐标为A(8,0),点B在y轴正半轴上,且AB=10,点P是△AOB外接圆上一点,且∠BOP=45°,则点P的坐标为( )
如图,点A的坐标为A(8,0),点B在y轴正半轴上,且AB=10,点P是△AOB外接圆上一点,且∠BOP=45°,则点P的坐标为( )| A. | (7,7) | B. | (7$\sqrt{2}$,7$\sqrt{2}$) | C. | (5$\sqrt{2}$,5$\sqrt{2}$) | D. | (5,5) |
| A. | 6048x4011 | B. | 6049x4034 | C. | 6049x4033 | D. | 6048x4035 |
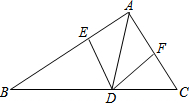 如图,已知S△ABC=40,AB=22,AC=18,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,则DE=2.
如图,已知S△ABC=40,AB=22,AC=18,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,则DE=2.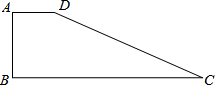 如图在四边形ABCD中,∠A=90°,AD=6,AB=8,BC=26,CD=24.
如图在四边形ABCD中,∠A=90°,AD=6,AB=8,BC=26,CD=24.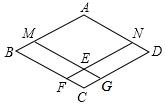 如图,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E.求证:
如图,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E.求证: