题目内容
1.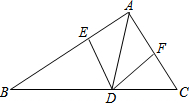 如图,已知S△ABC=40,AB=22,AC=18,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,则DE=2.
如图,已知S△ABC=40,AB=22,AC=18,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,则DE=2.
分析 根据角平分线的性质得到DE=DF,根据三角形的面积列方程即可得到结论.
解答 解:∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF,
∵S△ABC=$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=$\frac{1}{2}$DE•(AB+AC)=$\frac{1}{2}$×40•DE=40,
∴DE=2,
故答案为:2.
点评 本题考查了角平分线的性质,三角形的面积的计算,熟练掌握角平分线的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.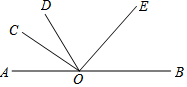 如图,已知点O在直线AB上,∠COE=90°,OD平分∠AOE,∠COD=25°,则∠BOD的度数为( )
如图,已知点O在直线AB上,∠COE=90°,OD平分∠AOE,∠COD=25°,则∠BOD的度数为( )
 如图,已知点O在直线AB上,∠COE=90°,OD平分∠AOE,∠COD=25°,则∠BOD的度数为( )
如图,已知点O在直线AB上,∠COE=90°,OD平分∠AOE,∠COD=25°,则∠BOD的度数为( )| A. | 100° | B. | 115° | C. | 65° | D. | 130° |
11. 如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )
如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )
 如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )
如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )| A. | 80° | B. | 100° | C. | 110° | D. | 120° |