题目内容
19.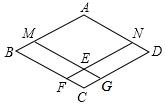 如图,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E.求证:
如图,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E.求证:(1)四边形AMEN是菱形;
(2)四边形EFCG是菱形.
分析 (1)由MG∥AD,NF∥AB,可证得四边形AMEN是平行四边形,又由四边形ABCD是菱形,BM=DN,可得AM=AN,即可证得四边形AMEN是菱形;
(2)先证明四边形EFCG是平行四边形,再证出CF=CG,即可得出四边形EFCG是菱形.
解答 证明:(1)∵MG∥AD,NF∥AB,
∴四边形AMEN是平行四边形,
∵四边形ABCD是菱形,
∴AB=AD,
∵BM=DN,
∴AB-BM=AD-DN,
∴AM=AN,
∴四边形AMEN是菱形;
(2)同(1)得:四边形BCGM、四边形CDNF是平行四边形,
∴MG∥BC,NF∥CD,BM=CG,DN=CF,
∴四边形EFCG是平行四边形,
∵BM=DN,
∴CF=CG,
∴四边形EFCG是菱形.
点评 此题考查了菱形的性质与判定、平行四边形的判定.证得四边形AMEN是菱形与四边形EFCG是菱形是关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
11. 如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )
如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )
 如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )
如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )| A. | 80° | B. | 100° | C. | 110° | D. | 120° |
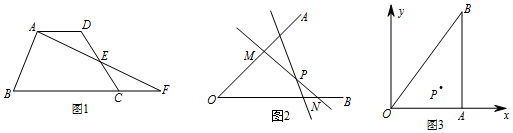
 如图,直线MN表示一条河,A、B代表河两岸的村庄,要在河上修一座桥,使它到两个村庄的距离之和最短,问桥应建在何处?请说明理由.
如图,直线MN表示一条河,A、B代表河两岸的村庄,要在河上修一座桥,使它到两个村庄的距离之和最短,问桥应建在何处?请说明理由.
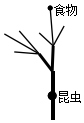 一只昆虫在如图所示的树枝上寻觅食物,假定昆虫在每个岔路口都会随机地选择一条路径,则它获得食物的概率是$\frac{1}{6}$.
一只昆虫在如图所示的树枝上寻觅食物,假定昆虫在每个岔路口都会随机地选择一条路径,则它获得食物的概率是$\frac{1}{6}$.