题目内容
19.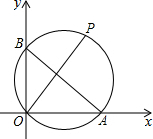 如图,点A的坐标为A(8,0),点B在y轴正半轴上,且AB=10,点P是△AOB外接圆上一点,且∠BOP=45°,则点P的坐标为( )
如图,点A的坐标为A(8,0),点B在y轴正半轴上,且AB=10,点P是△AOB外接圆上一点,且∠BOP=45°,则点P的坐标为( )| A. | (7,7) | B. | (7$\sqrt{2}$,7$\sqrt{2}$) | C. | (5$\sqrt{2}$,5$\sqrt{2}$) | D. | (5,5) |
分析 作PH⊥x轴于H,连结PA、PB,由A、B两点的坐标可求出AB,由△PAB和△POH都为等腰直角三角形,得出PA=$\frac{\sqrt{2}}{2}$AB,PH=OH,设OH=t,在在Rt△PHA中,运用勾股定理求出t的值,即可得出点P的坐标.
解答 解:作PH⊥x轴于H,连结PA、PB,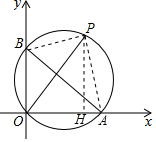
∵∠AOB=90°,
∴AB为△AOB外接圆的直径,
∴∠BPA=90°,
∵AB=10,∠BAP=∠BOP=45°,
∴PA=5$\sqrt{2}$,
设OH=t,则PH=t,AH=8-t,
在Rt△PHA中,
∵PH2+AH2=PA2,即t2+(8-t)2=(5$\sqrt{2}$)2,
解得,t1=1(舍去),t2=7,
∴点P的坐标为(7,7),
故选:A.
点评 本题考查的是圆周角定理及等腰直角三角形的性质,根据题意作出辅助线,构造出等腰直角三角形是解答此题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
9.有一个正方体,6个面上分别标有1~6这6个整数,投掷这个正方体一次,则出现向上一面的数字为偶数的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
10.已知一个等腰三角形两边长之比为1:4,周长为18,则这个等腰三角形底边长为( )
| A. | 2 | B. | 6 | C. | 8 | D. | 2或8 |
 李强家里搞装修时,木工师傅想要在一块矩形木板ABCD的中央挖去一个形状与原矩形相同,周长是原矩形一半的小矩形(如图),木工师傅算来算去,不知如何下手,正犯愁时,李强放学回家,见状说:“很方便,连接AC,BD交于点O,用刻度尺分别量出AO,BO,CO,DO的中点E,F,G,H,依次连接EF,FG,GH,HE,就得到要挖去的矩形EFGH.”请你说明道理.
李强家里搞装修时,木工师傅想要在一块矩形木板ABCD的中央挖去一个形状与原矩形相同,周长是原矩形一半的小矩形(如图),木工师傅算来算去,不知如何下手,正犯愁时,李强放学回家,见状说:“很方便,连接AC,BD交于点O,用刻度尺分别量出AO,BO,CO,DO的中点E,F,G,H,依次连接EF,FG,GH,HE,就得到要挖去的矩形EFGH.”请你说明道理.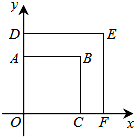 如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1:$\sqrt{2}$,点B的坐标为(1,1),则点E的坐标是($\sqrt{2}$,$\sqrt{2}$).
如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1:$\sqrt{2}$,点B的坐标为(1,1),则点E的坐标是($\sqrt{2}$,$\sqrt{2}$).