题目内容
6. 如图,△ABC是直角三角形,∠C=90°.
如图,△ABC是直角三角形,∠C=90°.(1)请作出△ABC的内切圆(⊙O尺规作图,不写作法,保留作图痕迹).
(2)设(1)中作出的⊙O与边AB、BC、CA分别相切于点D、E、F,BC=8,AC=6,求⊙O的面积.
分析 (1)首先由三角形的内心是三角形三个角平分线的交点,确定圆心,然后作边的垂线,确定半径,继而可求得△ABC的内切圆;
(2)由三角形的面积等于其内切圆的半径与周长积的一半,即可求得△ABC的内切圆的半径.
解答  解:(1)如图所示:⊙O即为所求;
解:(1)如图所示:⊙O即为所求;
(2)设△ABC内切圆的半径为r,
∵在Rt△ABC中,∠ACB=90°,AC=8,BC=6,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
∴S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×6×8=24,AB+AC+BC=24,
∵S△ABC=$\frac{1}{2}$(AB+AC+BC)r,
∴r=$\frac{{2S}_{△ABC}}{AB+AC+BC}$=$\frac{2×24}{24}$=2.
∴⊙O的面积=4π.
点评 此题主要考查了作图--复杂作图,关键是掌握三角形的内心是三角形角平分线的交点.

练习册系列答案
相关题目
 某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元,每天可售出40件,若每件降价10元,则每天多售出10件,请根据以上信息解答下列问题:
某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元,每天可售出40件,若每件降价10元,则每天多售出10件,请根据以上信息解答下列问题:
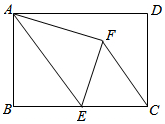 如图,在矩形ABCD中,AB=5,BC=8,点E为BC上一动点,把△ABE沿AE折叠;若点E是BC边的中点,点B落在点F处,连接CF.
如图,在矩形ABCD中,AB=5,BC=8,点E为BC上一动点,把△ABE沿AE折叠;若点E是BC边的中点,点B落在点F处,连接CF. 如图,矩形ABCD中,AB=4,BC=6,E是BC上一点(不与B、C重合),点P在边CD上运动,M、N分别是AE、PE的中点,线段MN长度的最大值是$\sqrt{13}$.
如图,矩形ABCD中,AB=4,BC=6,E是BC上一点(不与B、C重合),点P在边CD上运动,M、N分别是AE、PE的中点,线段MN长度的最大值是$\sqrt{13}$.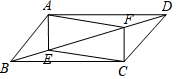 如图,在平行四边形ABCD中,E、F为对角线BD上两点,BE=DF,连接AE、EC、CF、FA.
如图,在平行四边形ABCD中,E、F为对角线BD上两点,BE=DF,连接AE、EC、CF、FA.