题目内容
14.已知,如图,在△ABC和△DEF(它们均为锐角三角形)中,AC=DF,AB=DE.(1)用尺规在图中分别作出AB、DE边上的高CG、FH(不要写作法,保留作图痕迹).
(2)如果CG=FH,猜测△ABC和△DEF是否全等,并说明理由.
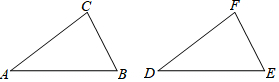
分析 (1)如图,以C为圆心,BC长为半径画弧交AB于点B′,作BB′垂直平分线即可.同理以F为圆心,EF长为半径画弧交DE于点E′,作EE′垂直平分线即可.
(2)猜测△ABC和△DEF全等,易证∠A=∠D,再证明△ABC≌△DEF即可.
解答 解:
(1)如图所示: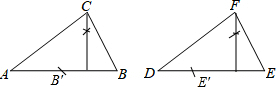
(2)△ABC≌△DEF,理由如下:
在Rt△CGA和Rt△FHD中,$\left\{\begin{array}{l}AC=DF\\ CG=FH\end{array}\right.$.
∴Rt△CGA≌△FHD(HL),
∴∠A=∠D.
在△ABC和△DEF中,
$\left\{\begin{array}{l}AB=DE\\∠A=∠D\\ AC=DF\end{array}\right.$,
∴△ABC≌△DEF(SAS).
点评 本题考查了全等三角形的判定与性质,应用与设计作图,熟练掌握三角形全等的判定方法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.某学校欲举办“校园运动挑战赛”,为此该校在三个年级中随机抽取一个班级进行了一次“你最喜欢的挑战项目”的问卷调查,每名学生都只选了一项.已知被调查的三个年级的学生人数均为50人,根据收集到的数据,绘制成如下统计图表(不完整):

根据统计图表中的信息,解答下列问题:
(1)在本次随机调查中,七年级抽查班级中喜欢“跳绳”项目的学生有12人,九年级抽查班级中喜欢“乒乓球”项目的学生人数占本班人数的百分比为18%;
(2)请将条形统计图补充完整;
(3)若该校共有3000名学生(三个年级的学生人数都相等),请估计该校喜欢“羽毛球”项目的学生总人数.
| 项目 | 跳绳 | 踢毽子 | 乒乓球 | 羽毛球 | 其他 |
| 人数(人) | 14 | 10 | 8 | 6 |

根据统计图表中的信息,解答下列问题:
(1)在本次随机调查中,七年级抽查班级中喜欢“跳绳”项目的学生有12人,九年级抽查班级中喜欢“乒乓球”项目的学生人数占本班人数的百分比为18%;
(2)请将条形统计图补充完整;
(3)若该校共有3000名学生(三个年级的学生人数都相等),请估计该校喜欢“羽毛球”项目的学生总人数.
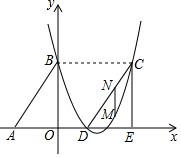 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,0为坐标原点,A、B两点的坐标分别为(-3,0))、(0,4),抛物线y=$\frac{2}{3}$x2+bx+c经过点B,且顶点在直线x=$\frac{5}{2}$上.
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,0为坐标原点,A、B两点的坐标分别为(-3,0))、(0,4),抛物线y=$\frac{2}{3}$x2+bx+c经过点B,且顶点在直线x=$\frac{5}{2}$上.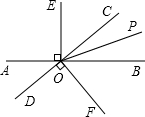 如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD
如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD 已知:如图,点G是CA的延长线上一点,CE交AB于点F,AD∥GE,且∠AGF=∠AFG.求证:AD平分∠BAC.
已知:如图,点G是CA的延长线上一点,CE交AB于点F,AD∥GE,且∠AGF=∠AFG.求证:AD平分∠BAC. 如图,△ABC是直角三角形,∠C=90°.
如图,△ABC是直角三角形,∠C=90°.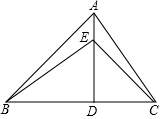 如图,锐角△ABC中,∠ABC=45°,AD是高,E为AD上一点,BE=AC.
如图,锐角△ABC中,∠ABC=45°,AD是高,E为AD上一点,BE=AC.