题目内容
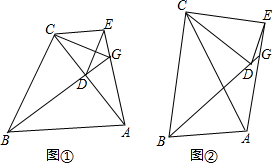
3.如图,CA=CB,CD=CE,∠ACB=∠DCE=α.(1)当α=60°,且点D在AC上,连BD、AE,相交于点G,如图①,求∠BGA.
(2)若0°<α<90°,如图②,求∠BGC.
分析 (1)由SAS证明△BCD≌△ACE,得出对应角相等∠CBD=∠CAE,由三角形的外角性质证出∠BCA=∠BGA,即可得出结果;
(2)证出∠BCD=∠ACE,由SAS证明△BCD≌△ACE,得出∠CBD=∠CAE,证出A、B、C、G四点共圆,由圆周角定理得出∠BGC=∠BAC,再由等腰三角形的性质和三角形内角和定理即可得出结果.
解答 解:(1)在△BCD和△ACE中,
$\left\{\begin{array}{l}{AC=CB}&{\;}\\{∠ACB=∠DCE}&{\;}\\{∠CD=CE}&{\;}\end{array}\right.$,
∴△BCD≌△ACE(SAS),
∴∠CBD=∠CAE,
∵∠CDG=∠CBD+∠BCD=∠CAE+∠BGA,
∴∠BCA=∠BGA,
∴∠BGA=60°;
(2)∵∠BCA=∠DCE,
∴∠ACB=∠DCE,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
$\left\{\begin{array}{l}{AC=CB}&{\;}\\{∠ACB=∠DCE}&{\;}\\{∠CD=CE}&{\;}\end{array}\right.$,
∴△BCD≌△ACE(SAS),
∴∠CBD=∠CAE,
∴A、B、C、G四点共圆,
∴∠BGC=∠BAC,
∵∠BCA=α,BC=AC,
∴∠BAC=$\frac{1}{2}$(180°-α),
∴∠BGC=∠BAC=$\frac{1}{2}$(180°-α).
点评 本题考查了全等三角形的判定与性质、三角形的外角性质、四点共圆、圆周角定理、等腰三角形的性质、三角形内角和定理等知识;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 小张想测量某建筑物AB的高度,在C处测得建筑物顶部A的仰角为30°,然后沿CB前进100米到达D处,测得顶部A的仰角为60°,求建筑物AB的高度.(结果保留根号)
小张想测量某建筑物AB的高度,在C处测得建筑物顶部A的仰角为30°,然后沿CB前进100米到达D处,测得顶部A的仰角为60°,求建筑物AB的高度.(结果保留根号)
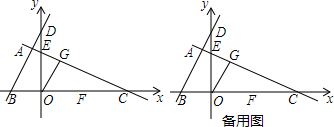
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的有( )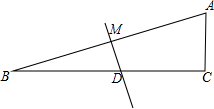 如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于点D,交AB于点M,BD=8cm,求AC的长.
如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于点D,交AB于点M,BD=8cm,求AC的长.