题目内容
15.如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求直径CD的长.
分析 本题应用垂径定理,由AB=10得AE=5,在Rt△OEA中,设半径为R,应用勾股定理得:R2=52+(R-1)2,继而求得CD的长.
解答 解:∵CD是⊙O的直径,AB⊥CD
∴AE=BE
∵AB=10
∴AE=5
设OA=R
∴OE=R-1
根据勾股定理:R2=52+(R-1)2
解得R=13
∴CD=2R=26
点评 本题是圆的学习中常见的一类题型,解决本题须熟练掌握垂径定理这一知识点,活学活用,难度不大.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
3.已知一个圆锥形的漏斗侧面展开图的圆心角为120°,圆锥的高为4.则圆锥的全面积( )
| A. | 6π | B. | 8π | C. | 16π | D. | 20π |
10.在直角三角形ABC中,∠C=90°,AC=3,BC=4 若以C为圆心,以2.5为半径做圆C,则圆C与AB所在直线的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 不能确定 |
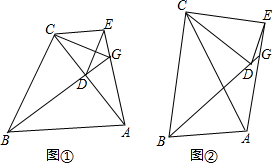
 如图,这个图形是一个平行四边形和一个直角梯形拼接成的图形,在该图中划一条直线,使该直线正好平分整个图形的面积,并说明划法和相应的理由.
如图,这个图形是一个平行四边形和一个直角梯形拼接成的图形,在该图中划一条直线,使该直线正好平分整个图形的面积,并说明划法和相应的理由.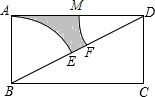 如图,已知矩形ABCD中,AB=8,BC=5π.分别以B,D为圆心,AB为半径画弧,两弧分别交对角线BD于点E,F,则图中阴影部分的面积为4π.
如图,已知矩形ABCD中,AB=8,BC=5π.分别以B,D为圆心,AB为半径画弧,两弧分别交对角线BD于点E,F,则图中阴影部分的面积为4π.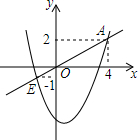 如图,二次函数y=x2+bx+c的图象与正比例函数y=kx的图象相交于点A(4,2)和点B(m,-1),求该二次函数与正比例函数的解析式.
如图,二次函数y=x2+bx+c的图象与正比例函数y=kx的图象相交于点A(4,2)和点B(m,-1),求该二次函数与正比例函数的解析式.