题目内容
19. 如图,直线AB∥DE,直线MN交直线AB于点A,交DE于点H,CH⊥DE于点H,若∠MAB=145°,则∠NHC=55°.
如图,直线AB∥DE,直线MN交直线AB于点A,交DE于点H,CH⊥DE于点H,若∠MAB=145°,则∠NHC=55°.
分析 先根据补角的定义求出∠BAH的度数,再由平行线的性质得出∠EHN的度数,根据CH⊥DE于点H可得出∠CHE=90°,据此可得出结论.
解答 解:∵∠MAB=145°,
∴∠BAH=180°-145°=35°.
∵直线AB∥DE,
∴∠EHN=∠BAH=35°.
∵CH⊥DE于点H,
∴∠CHE=90°,
∴∠NCH=90°-35°=55°.
故答案为:55°.
点评 本题考查的平行线的性质,用到的知识点为:两直线平行,同位角相等.

练习册系列答案
相关题目
11.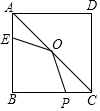 如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )
如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )
 如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )
如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )| A. | 4+3$\sqrt{2}$ | B. | $\sqrt{29}$+$\sqrt{5}$ | C. | 2+$\sqrt{5}$+3$\sqrt{2}$ | D. | $\sqrt{5}$+$\sqrt{2}$ |
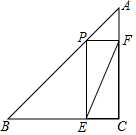 如图,△ABC是等腰直角三角形,∠C=90°,AC=BC=4,点P是AB上的一个动点(点P与点A、B不重合),过点P分别作PE⊥BC于点E,PF⊥AC于点F,连接EF.
如图,△ABC是等腰直角三角形,∠C=90°,AC=BC=4,点P是AB上的一个动点(点P与点A、B不重合),过点P分别作PE⊥BC于点E,PF⊥AC于点F,连接EF.