题目内容
11．
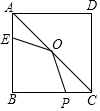如图，在正方形ABCD中，边长为4，E为AB上的点，且AE=1，O为AC的中点，P为BC上的动点，则△EOP周长的最小值是（ ）| A． | 4+3$\sqrt{2}$ | B． | $\sqrt{29}$+$\sqrt{5}$ | C． | 2+$\sqrt{5}$+3$\sqrt{2}$ | D． | $\sqrt{5}$+$\sqrt{2}$ |
分析 如图，作E关于直线BC的对称点E′，连接OE′交BC于P，连接PE，则此时△PEO的周长最小，求出三角形的三边的长即可．
解答 解：如图
作E关于直线BC的对称点E′，连接OE′交BC于P，连接PE，则此时△PEO的周长最小．
作OH⊥AB于H．在Rt△EOH中，易知OH=2，EH=1，OE=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$，
在Rt△OHE′中，易知HE′=5，OH=2，OE′=$\sqrt{{5}^{2}+{2}^{2}}$=$\sqrt{29}$，
∴△EOP的周长的最小值为$\sqrt{29}$+$\sqrt{5}$．
故选B．
点评 本题考查轴对称、正方形的性质、两点之间线段最短、勾股定理等知识，解题的关键是学会利用对称解决最值问题，属于中考常考题型．
练习册系列答案
相关题目
如图，直线AB∥DE，直线MN交直线AB于点A，交DE于点H，CH⊥DE于点H，若∠MAB=145°，则∠NHC=55°．
如图，OP平分∠AOB，∠AOP=15°，PC∥OA，PD⊥OA于点D，PD=2，求PC的长．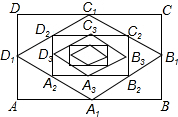
如图，在矩形ABCD中，AB=16，BC=12，顺次连结各边中点，得菱形A1B1C1D1；再顺次连结菱形A1B1C1D1的各边中点，得矩形A2B2C2D2；再顺次连结矩形A2B2C2D2的各边中点，得菱形A3B3C3D3；…这样继续下去．则图中的四边形A8B8C8D8的周长等于4，图中的四边形AnBnCnDn的面积等于192×（$\frac{1}{2}$）n．