题目内容
14.定义:到三角形两个顶点距离相等的点,叫做此三角形的准外心,如图,若PA=PB,则点P为△ABC的准外心,已知,如图,在△ABC中,∠A为直角,BC=5,AB=3.(1)若△ABC的一个准外心P在AC边上,试用尺规找出点P的位置(保留痕迹,不写作法);
(2)求线段PA的长.

分析 (1)首先正确理解准外心的定义,然后画图:①点P到A、C两点距离相等;②P到B、C两点距离相等.
(2)首先利用勾股定理计算出AC长,然后再分三种情况:①PB=BC;②PA=PC;③PA=PB进行计算.
解答 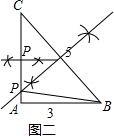 解:(1)如图所示;
解:(1)如图所示;
(2)∵BC=5,AB=3,
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=4,
①若PB=BC,设PA=x,则x2+32=(4-x)2,
解得:x=$\frac{7}{8}$,
即PA=$\frac{7}{8}$,
②若PA=PC,则PA=2;
③若PA=PB,由图知,在△PAB中,不可能,
综上PA=2或$\frac{7}{8}$.
点评 此题主要考查了复杂作图,以及勾股定理的应用,关键是正确理解题意,然后再分类讨论.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
5.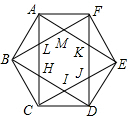 如图,正六边形ABCDEF的边长为6,连接对角线AC,BD,CE,DF,EA,FB,这些对角线相交得到正六边形HUKML,则得到的正六边形HUKML的面积为( )
如图,正六边形ABCDEF的边长为6,连接对角线AC,BD,CE,DF,EA,FB,这些对角线相交得到正六边形HUKML,则得到的正六边形HUKML的面积为( )
 如图,正六边形ABCDEF的边长为6,连接对角线AC,BD,CE,DF,EA,FB,这些对角线相交得到正六边形HUKML,则得到的正六边形HUKML的面积为( )
如图,正六边形ABCDEF的边长为6,连接对角线AC,BD,CE,DF,EA,FB,这些对角线相交得到正六边形HUKML,则得到的正六边形HUKML的面积为( )| A. | 18$\sqrt{3}$ | B. | 36$\sqrt{3}$ | C. | $\frac{9\sqrt{3}}{2}$ | D. | $\frac{18\sqrt{3}}{2}$ |
2. 如图,在平面直角坐标系中,⊙O的半径为2,AC,BD是⊙O的两条互相垂直的弦,垂足为M(1,$\sqrt{2}$),则四边形ABCD面积最大值为( )
如图,在平面直角坐标系中,⊙O的半径为2,AC,BD是⊙O的两条互相垂直的弦,垂足为M(1,$\sqrt{2}$),则四边形ABCD面积最大值为( )
 如图,在平面直角坐标系中,⊙O的半径为2,AC,BD是⊙O的两条互相垂直的弦,垂足为M(1,$\sqrt{2}$),则四边形ABCD面积最大值为( )
如图,在平面直角坐标系中,⊙O的半径为2,AC,BD是⊙O的两条互相垂直的弦,垂足为M(1,$\sqrt{2}$),则四边形ABCD面积最大值为( )| A. | 2$\sqrt{6}$ | B. | 5 | C. | 4 | D. | 6 |
19.下列计算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | 32=6 | C. | (-1)2015=-1 | D. | |-2|=-2 |
3.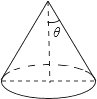 已知圆锥的底面半径为3cm,侧面积为15πcm2,设圆锥的母线与高的夹角为θ(如图所示),则tanθ的值为( )
已知圆锥的底面半径为3cm,侧面积为15πcm2,设圆锥的母线与高的夹角为θ(如图所示),则tanθ的值为( )
 已知圆锥的底面半径为3cm,侧面积为15πcm2,设圆锥的母线与高的夹角为θ(如图所示),则tanθ的值为( )
已知圆锥的底面半径为3cm,侧面积为15πcm2,设圆锥的母线与高的夹角为θ(如图所示),则tanθ的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
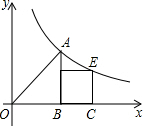 在平面直角坐标系中,等腰直角△OAB的直角边OB和正方形BCEF的一边BC都在x轴的正半轴上,函数y=$\frac{k}{x}$(k>0)的图象过点A,E.若BC=1,则k的值等于$\frac{3+\sqrt{5}}{2}$.
在平面直角坐标系中,等腰直角△OAB的直角边OB和正方形BCEF的一边BC都在x轴的正半轴上,函数y=$\frac{k}{x}$(k>0)的图象过点A,E.若BC=1,则k的值等于$\frac{3+\sqrt{5}}{2}$.