题目内容
5.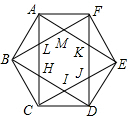 如图,正六边形ABCDEF的边长为6,连接对角线AC,BD,CE,DF,EA,FB,这些对角线相交得到正六边形HUKML,则得到的正六边形HUKML的面积为( )
如图,正六边形ABCDEF的边长为6,连接对角线AC,BD,CE,DF,EA,FB,这些对角线相交得到正六边形HUKML,则得到的正六边形HUKML的面积为( )| A. | 18$\sqrt{3}$ | B. | 36$\sqrt{3}$ | C. | $\frac{9\sqrt{3}}{2}$ | D. | $\frac{18\sqrt{3}}{2}$ |
分析 由正六边形的性质得出△ACE的面积=$\frac{1}{2}$正六边形的面积=27$\sqrt{3}$,△ALM的面积+△CHI的面积+△EKJ的面积=$\frac{1}{3}$△ACE的面积=9$\sqrt{3}$,即可得出结果.
解答 解:由正六边形的性质得:△ACE的面积=$\frac{1}{2}$正六边形的面积=$\frac{1}{2}$×6×$\frac{1}{2}$×6×6×sin60°=27$\sqrt{3}$,
△ALM的面积+△CHI的面积+△EKJ的面积=$\frac{1}{3}$△ACE的面积=9$\sqrt{3}$,
∴正六边形HUKML的面积=27$\sqrt{3}$-9$\sqrt{3}$=18$\sqrt{3}$;
故答案为:A.
点评 本题考查了正六边形的性质;利用正六边形可分成6个全等的等边三角形,由正六边形的性质得出三角形和正六边形的面积关系是解决问题的关键.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
13.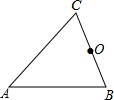 如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( )
如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( )
 如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( )
如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
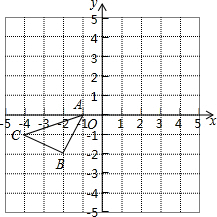 如图,所示的正方形网格中,△ABC的顶点均在格点上,在所给平面直角坐标系中解答下列问题:
如图,所示的正方形网格中,△ABC的顶点均在格点上,在所给平面直角坐标系中解答下列问题:
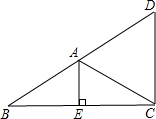 已知:如图AE⊥BC,∠EAC=∠ACD,试说明BC垂直于DC.
已知:如图AE⊥BC,∠EAC=∠ACD,试说明BC垂直于DC.