题目内容
9.若x是不等于1的实数,我们把$\frac{1}{1-x}$称为x的差倒数,如2的差倒数是$\frac{1}{1-2}$=-1,-1的差倒数为$\frac{1}{1-(-1)}$=$\frac{1}{2}$.现已知x1=-$\frac{1}{3}$,x2是x1的差倒数,x3是x2的差倒数,x4是x3的差倒数,…,依此类推,则x2016的值为4.分析 根据差倒数的定义找出该组数列的前4个数,由x4=x1,从而得出数据变化规律,根据规律可得出x2016的值.
解答 解:根据差倒数的定义可得出:
${x}_{1}=-\frac{1}{3}$,x2=$\frac{1}{1-(-\frac{1}{3})}$=$\frac{3}{4}$,x3=$\frac{1}{1-\frac{3}{4}}$=4,x4=$\frac{1}{1-4}$=-$\frac{1}{3}$,…
由此发现该组数每3个一循环.
∵2016÷3=672,
∴x2016=x3=4.
故答案为:4.
点评 本题考查了数字的变化以及求倒数,解题的关键是发现“该组数每3个一循环”这个规律.本题属于基础题,难度不大,根据差倒数的定义式列出前4个数据即可找出规律得以解决.

练习册系列答案
相关题目
1.已知(x+a)(x+b)=x2-13x+36,则a+b=( )
| A. | -5 | B. | 5 | C. | -13 | D. | -13或5 |
19.一个正方形的面积为21,它的边长为a,则a-1的边长大小为( )
| A. | 2与3之间 | B. | 3与4之间 | C. | 4与5之间 | D. | 5与6之间 |
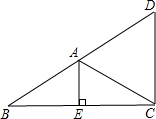 已知:如图AE⊥BC,∠EAC=∠ACD,试说明BC垂直于DC.
已知:如图AE⊥BC,∠EAC=∠ACD,试说明BC垂直于DC.