题目内容
2. 如图,在平面直角坐标系中,⊙O的半径为2,AC,BD是⊙O的两条互相垂直的弦,垂足为M(1,$\sqrt{2}$),则四边形ABCD面积最大值为( )
如图,在平面直角坐标系中,⊙O的半径为2,AC,BD是⊙O的两条互相垂直的弦,垂足为M(1,$\sqrt{2}$),则四边形ABCD面积最大值为( )| A. | 2$\sqrt{6}$ | B. | 5 | C. | 4 | D. | 6 |
分析 解答本题要注意当AC、BD相等,且OM平分两弦的相交的角时,此时四边形ABCD的面积最大,求出对角线AC、BD的长度可以求得四边形ABCD的最大面积.
解答 解:当AC、BD相等,且OM平分两弦的相交的角时,这时O到弦的距离为:OM×sin45=$\frac{\sqrt{6}}{2}$,
由勾股定理及垂径定理知弦长为:$\sqrt{10}$,
S=$\frac{1}{2}$×$\sqrt{10}$×$\sqrt{10}$=5;
故选B.
点评 本题考查了垂径定理以及坐标与图形的变换,当对角线互相垂直时,四边形的面积等于对角线乘积的一半,这一性质要好好记忆,同时还要注意极值图形的选取方法.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
13.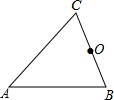 如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( )
如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( )
 如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( )
如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
7.若a=b-3,则b-a的值是( )
| A. | -3 | B. | 3 | C. | 0 | D. | 6 |
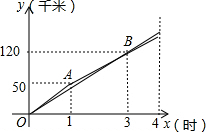 甲、乙两名自行车运动员在同一条直线公路上进行骑自行车训练,他们同时同地同向出发,乙在行驶过程中改变了一次速度,甲、乙两人各自在公路上训练时行驶路程y(千米)与行驶时间x(时)(0≤x≤4)之间的函数图象如图所示.
甲、乙两名自行车运动员在同一条直线公路上进行骑自行车训练,他们同时同地同向出发,乙在行驶过程中改变了一次速度,甲、乙两人各自在公路上训练时行驶路程y(千米)与行驶时间x(时)(0≤x≤4)之间的函数图象如图所示.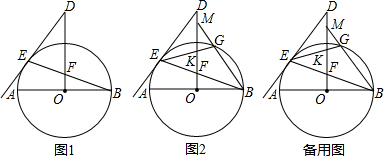
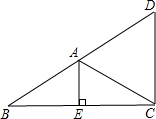 已知:如图AE⊥BC,∠EAC=∠ACD,试说明BC垂直于DC.
已知:如图AE⊥BC,∠EAC=∠ACD,试说明BC垂直于DC.
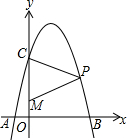 如图,抛物线y=-x2+4x+5与x轴交于A、B两点,与y轴交于点C.已知M(0,1),点P是第一象限内的抛物线上的动点.△PCM是以CM为底的等腰三角形,则点P的坐标为(2+$\sqrt{6}$,3).
如图,抛物线y=-x2+4x+5与x轴交于A、B两点,与y轴交于点C.已知M(0,1),点P是第一象限内的抛物线上的动点.△PCM是以CM为底的等腰三角形,则点P的坐标为(2+$\sqrt{6}$,3).