题目内容
13.一元二次方程4x2-1=4x的根的情况是( )| A. | 有两个不相等的实数根 | B. | 只有一个实数根 | ||
| C. | 有两个相等的实数根 | D. | 没有实数根 |
分析 首先求得△=b2-4ac的值,继而判定一元二次方程4x2-1=4x的根的情况.
解答 解:∵4x2-1=4x,
∴4x2-4x-1=0,
∴a=4,b=-4.c=-1,
∴△=b2-4ac=(-4)2-4×4×(-1)=32>0,
∴有两个不相等的实数根.
故选A.
点评 此题考查了根的判别式.注意一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.某商家经销一种绿茶,用于装修门面已投资3000元.已知绿茶每千克成本50元,经研究发现销量y(kg)随销售单价x(元/kg)的变化而变化,具体变化规律如表所示:
设该绿茶的月销售利润为w(元)(销售利润=单价×销售量-成本)
(1)请根据上表,写出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求w与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,w的值最大?
(3)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于80元,要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元,那么第二个月时里应该确定销售单价在什么范围内?
| 销售单价x(元/kg) | … | 70 | 75 | 80 | 85 | 90 | … |
| 月销售量y(kg) | … | 100 | 90 | 80 | 70 | 60 | … |
(1)请根据上表,写出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求w与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,w的值最大?
(3)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于80元,要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元,那么第二个月时里应该确定销售单价在什么范围内?
4.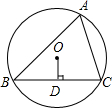 如图,△ABC内接于⊙O,作OD⊥BC于点D,若∠A=60°,则OD:CD的值为( )
如图,△ABC内接于⊙O,作OD⊥BC于点D,若∠A=60°,则OD:CD的值为( )
 如图,△ABC内接于⊙O,作OD⊥BC于点D,若∠A=60°,则OD:CD的值为( )
如图,△ABC内接于⊙O,作OD⊥BC于点D,若∠A=60°,则OD:CD的值为( )| A. | 1:2 | B. | 1:$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | 2:$\sqrt{3}$ |
8. 若函数y=kx+b的图象如图所示,则关于x的不等式k(x+3)+b<0的解集为( )
若函数y=kx+b的图象如图所示,则关于x的不等式k(x+3)+b<0的解集为( )
 若函数y=kx+b的图象如图所示,则关于x的不等式k(x+3)+b<0的解集为( )
若函数y=kx+b的图象如图所示,则关于x的不等式k(x+3)+b<0的解集为( )| A. | x<2 | B. | x>2 | C. | x<-1 | D. | x>-1 |
18.一元二次方程x2+3x+1=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 只有一个实数根 |
5.将某班级全体同学按课外阅读的不同兴趣分成三组,情况如表格所示,则表中a的值应该是7.
| 第一组 | 第二组 | 第三组 | |
| 频数 | 12 | 16 | a |
| 频率 | b | c | 20% |
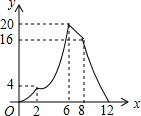
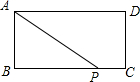 如图,在矩形ABCD中,AB=2,AD=4,矩形边上一动点P沿A→B→C→D→A的路径移动.设点P经过的路径长为x,AP2=y,则下列能大致反映y与x的函数关系的图象是( )
如图,在矩形ABCD中,AB=2,AD=4,矩形边上一动点P沿A→B→C→D→A的路径移动.设点P经过的路径长为x,AP2=y,则下列能大致反映y与x的函数关系的图象是( )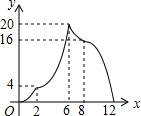
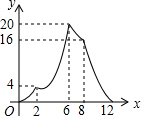

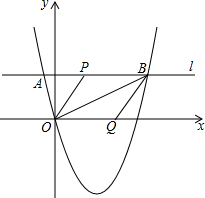 如图,抛物线y=ax2+3(a-1)x(a>0)经过点A(-3,m),过点A作直线l平行于x轴与抛物线交于另一点B,在x轴上取点Q,连接BQ,使得∠QBO=∠ABO,过点O作OP平行BQ交l于点P,若AP=$\frac{1}{2}$AB,则a的值为$\frac{1}{9}$.
如图,抛物线y=ax2+3(a-1)x(a>0)经过点A(-3,m),过点A作直线l平行于x轴与抛物线交于另一点B,在x轴上取点Q,连接BQ,使得∠QBO=∠ABO,过点O作OP平行BQ交l于点P,若AP=$\frac{1}{2}$AB,则a的值为$\frac{1}{9}$.