题目内容
8. 若函数y=kx+b的图象如图所示,则关于x的不等式k(x+3)+b<0的解集为( )
若函数y=kx+b的图象如图所示,则关于x的不等式k(x+3)+b<0的解集为( )| A. | x<2 | B. | x>2 | C. | x<-1 | D. | x>-1 |
分析 先把(2,0)代入y=kx+b得b=-2k,则不等式化为k(x+3)-2k<0,然后在k<0的情况下解不等式即可.
解答 解:把(2,0)代入y=kx+b得2k+b=0,则b=-2k,
所以k(x+3)+b<0化为k(x+3)-2k<0,
即kx+k<0,
因为k<0,
所以x>-1.
故选D.
点评 本题考查了一次函数与一元一次不等式:一次函数与一元一次不等式的关系从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
18. 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )
 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )| A. | 20 | B. | 22 | C. | 14 | D. | 16 |
19.观察下列图形规律:当n=( )时,图形“•”的个数和“△”的个数相等

| A. | 9 | B. | 7 | C. | 6 | D. | 5 |
16. 如图,在Rt△ABC中,∠C=90°,∠B=30°,将Rt△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角最小为( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,将Rt△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角最小为( )
 如图,在Rt△ABC中,∠C=90°,∠B=30°,将Rt△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角最小为( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,将Rt△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角最小为( )| A. | 115° | B. | 125° | C. | 120° | D. | 145° |
3. 如图,已知圆心角∠BOC=100°,则圆周角∠BAC的大小是( )
如图,已知圆心角∠BOC=100°,则圆周角∠BAC的大小是( )
 如图,已知圆心角∠BOC=100°,则圆周角∠BAC的大小是( )
如图,已知圆心角∠BOC=100°,则圆周角∠BAC的大小是( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
13.一元二次方程4x2-1=4x的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 只有一个实数根 | ||
| C. | 有两个相等的实数根 | D. | 没有实数根 |
20.某校举行“我爱我校”演讲比赛,由7名学生组成评委组.小明统计了每位评委对某参赛选手的评分并制成如下表格:
如果以去掉一个最高分和一个最低分后其他5名评委的平均分记为选手的最后得分,那么表中的数据一定不发生变化的是( )
| 众数 | 中位数 | 平均数 | 方差 |
| 7.9 | 8.3 | 8.2 | 0.3 |
| A. | 众数 | B. | 中位数 | C. | 平均数 | D. | 方差 |
6.若一个多边形的每个内角都为135°,则它的边数为( )
| A. | 6 | B. | 8 | C. | 5 | D. | 10 |
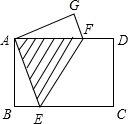 如图,矩形纸片ABCD中,AB=3cm,BC=4cm,现将A、C重合,使纸片折叠压平,设折痕为EF,试确定重叠部分的△AEF的面积是$\frac{25}{16}$.
如图,矩形纸片ABCD中,AB=3cm,BC=4cm,现将A、C重合,使纸片折叠压平,设折痕为EF,试确定重叠部分的△AEF的面积是$\frac{25}{16}$.