题目内容

11．计算sin30°+cos245°=1．

分析 把特殊角的三角函数值代入计算即可．

解答 解：原式=$\frac{1}{2}$+（$\frac{\sqrt{2}}{2}$）2
=$\frac{1}{2}$+$\frac{1}{2}$
=1，
故答案为：1．

点评 本题考查的是特殊角是三角函数值的计算，熟记30°、45°、60°角的各种三角函数值是解题的关键．

练习册系列答案
相关题目
13．一元二次方程4x2-1=4x的根的情况是（　　）
A．有两个不相等的实数根B．只有一个实数根
C．有两个相等的实数根D．没有实数根
2．如果$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程x-3y=-3的一组解，那么代数式5-a+3b的值是（　　）
A．8B．5C．2D．0
19．在下列二次根式：$\sqrt{\frac{1}{3}}$，$\sqrt{2}$+$\sqrt{5}$，$\sqrt{{a}^{2}+{b}^{2}}$，$\sqrt{3ab}$中，是最简二次根式的有（　　）
A．1个B．2个C．3个D．4个
6．若一个多边形的每个内角都为135°，则它的边数为（　　）
A．6B．8C．5D．10
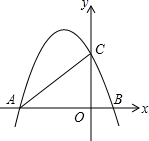16．如图，抛物线y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C，连接AC、BC．
（1）抛物线的顶点坐标是（-$\frac{3}{2}$，$\frac{25}{8}$）；
（2）①求A、B两点的坐标；
②猜想AC与BC的位置关系，并说明理由；
（3）如果点P是抛物线对称轴上的一个动点，当点P到B、C两点的距离之差最大时，求P点的坐标．
3．方程组$\left\{\begin{array}{l}{y=x}\\{3x+y=4}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$．
20．如图，四边形ABCD是菱形，点E，点F分别是CD，AD上的点，CE=DF，DE=2CE，AE，CF交于点O，则AO：OE=6．
1．把下列有理式中，是分式的代号填在横线上②⑤⑥．
①-3x；②$\frac{x}{y}$；③$\frac{2}{3}{x^2}y-7x{y^2}$；④-$\frac{1}{8}x$；⑤$\frac{5}{y+3}$；⑥$\frac{{{x^2}-1}}{x-1}$；⑦-$\frac{{{m^2}-1}}{π}$；⑧$\frac{3m+2}{0.5}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网