题目内容
3.某商家经销一种绿茶,用于装修门面已投资3000元.已知绿茶每千克成本50元,经研究发现销量y(kg)随销售单价x(元/kg)的变化而变化,具体变化规律如表所示:| 销售单价x(元/kg) | … | 70 | 75 | 80 | 85 | 90 | … |
| 月销售量y(kg) | … | 100 | 90 | 80 | 70 | 60 | … |
(1)请根据上表,写出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求w与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,w的值最大?
(3)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于80元,要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元,那么第二个月时里应该确定销售单价在什么范围内?
分析 (1)设y=kx+b,待定系数法求解即可得;
(2)根据:“总利润=每千克利润×销售量”列出函数关系式,配方可得其最值情况;
(3)由(2)知,第二个月利润需达到1700+550即W=2250才能满足题目条件,解方程可得x的值,根据二次函数性质可得x的取值范围.
解答 解:(1)设y=kx+b,
将(70,100),(75,90)代入上式,
得:$\left\{\begin{array}{l}70k+b=100\\ 75k+b=90\end{array}\right.$
解得:$\left\{\begin{array}{l}k=-2\\ b=240\end{array}\right.$,
则y=-2x+240,
(2)w=(x-50)y
=(x-50)(-2x+240)
=-2x2+340x-9000
=-2(x-85)2+2450,
当x=85时,w最大=2450;
(3)由(2)知,第1个月还有3000-2450=550元的投资成本没有收回.
则要想在全部收投资的基础上使第二个月的利润达到1700元,
即w=2250才可以,
可得方程:-2(x-85)2+2450=2250
解得:x1=75,x2=95
根据题意x2=95不合题意,应舍去,
当x=80时,y=2400,
∵-2<0,
∴当x<85时,w随x的增大而增大,
当w≥2250,且销售单价不高于80时,75≤x≤80.
答:当销售单价为75≤x≤80元时,在全部收回投资的基础上使第二个月的利润不低于1700元.
点评 本题主要考查二次函数的实际应用能力及待定系数求一次函数解析式,根据题意准确抓住相等关系列出函数关系式是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
18. 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )
 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )| A. | 20 | B. | 22 | C. | 14 | D. | 16 |
8.已知$\frac{a}{b}=\frac{5}{13}$,则$\frac{a-b}{a+b}$的值是( )
| A. | $-\frac{2}{3}$ | B. | $-\frac{3}{2}$ | C. | $-\frac{9}{4}$ | D. | $-\frac{4}{9}$ |
15.如图是某几何体的三视图,其侧面积( )


| A. | 2 | B. | 4 | C. | 2π | D. | π+2 |
12.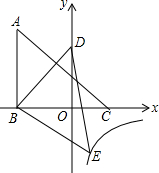 如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )
 如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )| A. | -3 | B. | -4 | C. | -5 | D. | -3$\sqrt{2}$ |
13.一元二次方程4x2-1=4x的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 只有一个实数根 | ||
| C. | 有两个相等的实数根 | D. | 没有实数根 |