题目内容
4．
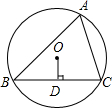如图，△ABC内接于⊙O，作OD⊥BC于点D，若∠A=60°，则OD：CD的值为（ ）| A． | 1：2 | B． | 1：$\sqrt{2}$ | C． | 1：$\sqrt{3}$ | D． | 2：$\sqrt{3}$ |
分析 连接OB，OC，根据圆周角定理求出∠BOC的度数，再由等腰三角形的性质求出∠COD的度数，进而可得出结论．
解答 
解：连接OB，OC，
∵∠A=60°，
∴∠BOC=2∠A=120°．
∵OB=OC，OD⊥BC，
∴∠COD=$\frac{1}{2}$∠BOC=60°，
∴$\frac{OD}{CD}$=cot60°=$\sqrt{3}$，即OD：CD=1：$\sqrt{3}$．
故选C．
点评 本题考查的是三角形的外接圆与外心，根据题意作出辅助线，利用圆周角定理求出∠BOC的度数是解答此题的关键．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
15．如图是某几何体的三视图，其侧面积（ ）
| A． | 2 | B． | 4 | C． | 2π | D． | π+2 |
12．
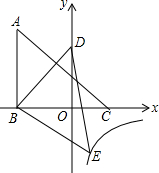如图，△ABC的三个顶点的坐标分别为A（-3，5），B（-3，0），C（2，0），将△ABC绕点B顺时针旋转一定的角度后得到△DBE，且使点D落在y轴上，与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上，则k的值为（ ）
如图，△ABC的三个顶点的坐标分别为A（-3，5），B（-3，0），C（2，0），将△ABC绕点B顺时针旋转一定的角度后得到△DBE，且使点D落在y轴上，与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上，则k的值为（ ）| A． | -3 | B． | -4 | C． | -5 | D． | -3$\sqrt{2}$ |
19．观察下列图形规律：当n=（ ）时，图形“•”的个数和“△”的个数相等
| A． | 9 | B． | 7 | C． | 6 | D． | 5 |
9．设二次函数y=ax2+bx+c（a≠0），当x=2时，函数值y=0，则方程ax2+bx+c=0的判别式△=b2-4ac必定是（ ）
| A． | △=0 | B． | △＜0 | C． | △＞0 | D． | △≥0 |
16．
如图，在Rt△ABC中，∠C=90°，∠B=30°，将Rt△ABC绕点A按顺时针方向旋转到△AB1C1的位置，使得点C、A、B1在同一条直线上，那么旋转角最小为（ ）
如图，在Rt△ABC中，∠C=90°，∠B=30°，将Rt△ABC绕点A按顺时针方向旋转到△AB1C1的位置，使得点C、A、B1在同一条直线上，那么旋转角最小为（ ）| A． | 115° | B． | 125° | C． | 120° | D． | 145° |
13．一元二次方程4x2-1=4x的根的情况是（ ）
| A． | 有两个不相等的实数根 | B． | 只有一个实数根 | ||
| C． | 有两个相等的实数根 | D． | 没有实数根 |