题目内容
4．在边长A的正方形中前去一个边长B的小正方形（A＞B），把剩下的部分制成一个梯形，请回答下列问题：
（1）这个拼图验证了一个乘法公式是（a+b）（a-b）=a2-b2．
（2）请利用这个公式计算：（1-$\frac{1}{{2}^{2}}$）（1-$\frac{1}{{3}^{2}}$）（1-$\frac{1}{{4}^{2}}$）（1-$\frac{1}{{5}^{2}}$）…（1-$\frac{1}{5{0}^{2}}$）
分析 （1）将阴影部分面积用含a，b的代数式表示出来，再根据阴影部分的面积相等得出乘法公式；
（2）根据所得的平方差公式，将计算式子中每个括号内进行因式分解，即可得出结果．
解答 解：（1）左图中，阴影部分面积=a2-b2
右图中，阴影部分面积=$\frac{（2b+2a）（a-b）}{2}$=（a+b）（a-b）
∴a2-b2=（a+b）（a-b）
故答案为：（a+b）（a-b）=a2-b2；
（2）原式=（1+$\frac{1}{2}$）×$（1-\frac{1}{2}）$）×（1+$\frac{1}{3}$）×（1-$\frac{1}{3}$）×（1-$\frac{1}{4}$）×（1+$\frac{1}{4}$）×…×（1+$\frac{1}{50}$）×（1-$\frac{1}{50}$）
=$\frac{3}{2}$×$\frac{1}{2}$×$\frac{4}{3}$×$\frac{2}{3}$×$\frac{3}{4}$×$\frac{5}{4}$×…×$\frac{51}{50}$×$\frac{49}{50}$
=$\frac{1}{2}$×$\frac{51}{50}$
=$\frac{51}{100}$
点评 本题主要考查了平方差公式的几何背景，解题时注意：利用图形的面积和作为相等关系列出等式即可验证平方差公式．
练习册系列答案
相关题目
如图，在正方形ABCD中，点E为边AB上任一点（与点A，B不重合），连接CE，过点D作DF⊥CE于点F，连接AF并延长交BC边于点G，连接EG，若正方形边长为4，GC=$\frac{2}{3}$AE，则GE=$\frac{4}{9}$$\sqrt{85}$．
如图，△ABC中，∠C=90°，D为BC的中点，∠ADC=60°，AC=$\sqrt{3}$．求△ABD的周长．
在给定坐标系内，画出函数y=（x-1）2的图象，并指出y随x增大而减小的x的取值范围．
16．图1中的摩天轮可抽象成一个圆，圆上一点离地面的高度y（m）与旋转时间x（min）之间的关系如图2所示，根据图中的信息，回答问题：
（1）根据图2补全表格：
（2）如表反映的两个变量中，自变量是旋转时间x，因变量是高度y；
（3）根据图象，摩天轮的直径为65m，它旋转一周需要的时间为6min．
（1）根据图2补全表格：
| 旋转时间x/min | 0 | 3 | 6 | 8 | 12 | … |
| 高度y/m | 5 | 70 | 5 | 54 | 5 | … |
（3）根据图象，摩天轮的直径为65m，它旋转一周需要的时间为6min．
求当a为何值时，代数式$\frac{5a+4}{6}$的值不大于代数式$\frac{7}{8}$-$\frac{1-a}{3}$的值？在数轴上表示解集，并求出满足条件的最大整数．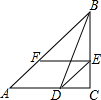
如图，在△ABC中，BD平分∠ABC交AC于点D，DE∥AB交BC于点E，EF∥AC交AB于点F，求证：BE=AF．