Question

15．如图，在正方形ABCD中，点E为边AB上任一点（与点A，B不重合），连接CE，过点D作DF⊥CE于点F，连接AF并延长交BC边于点G，连接EG，若正方形边长为4，GC=$\frac{2}{3}$AE，则GE=$\frac{4}{9}$$\sqrt{85}$．

Answer 1

分析 如图，延长DA、CE交于点M．假设AE=3a，GC=2a，想办法用a的代数式表示AM、CF、FM，由$\frac{CG}{AM}$=$\frac{CF}{FM}$，列出方程即可解决问题．

解答 解：如图，延长DA、CE交于点M．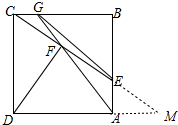

∵GC=$\frac{2}{3}$AE，可以假设AE=3a，GC=2a，
∵四边形ABCD 是正方形，
∴AB=BC=CD=AD=4，AB∥CD，BC∥AD，
∴$\frac{BC}{AM}$=$\frac{BE}{AE}$，
∴$\frac{4}{AM}$=$\frac{4-3a}{3a}$，
∴AM=$\frac{12a}{4-3a}$，
由△CDF∽△ECB，得$\frac{DC}{EC}$=$\frac{CF}{BE}$，
∴CF=$\frac{4（4-3a）}{\sqrt{{4}^{2}+（4-3a）^{2}}}$，
由△MDF∽△CEB，得$\frac{FM}{BC}$=$\frac{DM}{CE}$，
∴FM=$\frac{64}{（4-3a）\sqrt{{4}^{2}+（4-3a）^{2}}}$，
∵CG∥AM，
∴$\frac{CG}{AM}$=$\frac{CF}{FM}$，
∴$\frac{2a}{\frac{12a}{4-3a}}$=$\frac{\frac{4（4-3a）}{\sqrt{{4}^{2}+（4-3a）^{2}}}}{\frac{64}{（4-3a）\sqrt{{4}^{2}+（4-3a）^{2}}}}$，
解得a=$\frac{4}{9}$，
在Rt△GBE中，∵BG=4-$\frac{8}{9}$=$\frac{28}{9}$，BE=4-$\frac{12}{9}$=$\frac{24}{9}$，
∴GE=$\sqrt{B{G}^{2}+B{E}^{2}}$=$\sqrt{（\frac{28}{9}）^{2}+（\frac{24}{9}）^{2}}$=$\frac{4}{9}$$\sqrt{85}$，
故答案为$\frac{4}{9}$$\sqrt{85}$．

点评 本题考查正方形的性质、相似三角形的判定和性质、勾股定理等知识，解题的关键是学会利用参数，构建方程解决问题，属于中考常考题型．