题目内容
12.已知x13+x23+…+x83-x93的个位数字是1,其中,x1,x2,…,x9是2001,2002,2009中的九个不同的数,且8x9>x1+x2+…+x8,则x9=2008.分析 首先求得这九个数字的立方的位数和,然后将原式变形为(${{x}_{1}}^{3}+{x}_{2}^{3}+{x}_{3}^{3}+…+{x}_{9}^{3}$)-2${x}_{9}^{3}$,从而求得${x}_{9}^{3}$的个位数字是7或2,故此可知${x}_{9}^{3}$是2003或2008,然后再根据所给的不等式即可确定出x9的值.
解答 解:${x}_{1}^{3}+{x}_{2}^{3}+{x}_{3}^{3}+…+{x}_{8}^{3}$=(${{x}_{1}}^{3}+{x}_{2}^{3}+{x}_{3}^{3}+…+{x}_{9}^{3}$)-$2{x}_{9}^{3}$,
∵20013、20023、…20093的个位数字一次是1、8、7、4、5、6、3、2、9,
∴${{x}_{1}}^{3}+{x}_{2}^{3}+{x}_{3}^{3}+…+{x}_{9}^{3}$的个位数字一定是5.
又∵(${{x}_{1}}^{3}+{x}_{2}^{3}+{x}_{3}^{3}+…+{x}_{9}^{3}$)-$2{x}_{9}^{3}$的个位数字是1,
∴${x}_{9}^{3}$的个位数字是7或2,从而${x}_{9}^{3}$是2003或2008.
∵8x9>x1+x2+…+x8,
∴9x9>${{x}_{1}}^{3}+{x}_{2}^{3}+{x}_{3}^{3}+…+{x}_{9}^{3}$.
∴9x9>2005×9.
∴x9>2005.
∴x9=2008.
故答案为:2008.
点评 本题主要考查的是数字的尾数特征,将原式变形为(${{x}_{1}}^{3}+{x}_{2}^{3}+{x}_{3}^{3}+…+{x}_{9}^{3}$)-$2{x}_{9}^{3}$,然后根据尾数特点确定出x9的值是解题的关键.

 小明和小亮进行百米赛跑,小明比小亮跑得快.如果两人同时起跑,小明肯定赢.现在小明让小亮先跑若干米.途中l1,l2分别表示两人所跑路程与时间的关系.根据图象回答:
小明和小亮进行百米赛跑,小明比小亮跑得快.如果两人同时起跑,小明肯定赢.现在小明让小亮先跑若干米.途中l1,l2分别表示两人所跑路程与时间的关系.根据图象回答: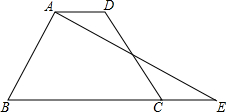 如图,在四边形ABCD中,点F是边CD上一点,连结AF,并延长AF交BC的延长线于点E,使得△ADF与△FCE全等.
如图,在四边形ABCD中,点F是边CD上一点,连结AF,并延长AF交BC的延长线于点E,使得△ADF与△FCE全等.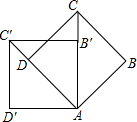 如图,正方形ABCD旋转后得到正方形AB′C′D′,①旋转角是45度;②若AB=1,则C′D=$\sqrt{2}$-1.
如图,正方形ABCD旋转后得到正方形AB′C′D′,①旋转角是45度;②若AB=1,则C′D=$\sqrt{2}$-1. 如图,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB.O为AD、CE的交点,求证:OE=OD.
如图,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB.O为AD、CE的交点,求证:OE=OD.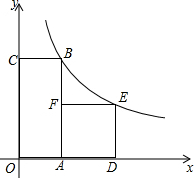 如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半釉上,点F在AB上,点B、E在反比例函数$y=\frac{k}{x}$的图象上OA=1,OC=4.
如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半釉上,点F在AB上,点B、E在反比例函数$y=\frac{k}{x}$的图象上OA=1,OC=4.