题目内容
17. 如图,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB.O为AD、CE的交点,求证:OE=OD.
如图,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB.O为AD、CE的交点,求证:OE=OD.
分析 过O作OM⊥AB,ON⊥BC,垂足分别为M、N,由条件可知O在∠B的平分线上,结合条件可求得∠EOD=∠MON=120°,可得到∠EOM=∠NOD,可证明△EOM≌△DON,可证明OD=OE.
解答 证明:如图,过O作OM⊥AB,ON⊥BC,垂足分别为M、N,
∵AD、CE为角平分线,
∴点O在∠B的平分线上,
∴OM=ON,
∵∠B=60°,
∴∠BAC+∠BCA=180°-60°=120°,
∵AD平分∠BAC,CE平分∠BCA,
∴∠BAC=2∠OAC,∠BCA=2∠OCA,
∴∠OAC+∠OCA=60°,
∴∠AOC=120°,
∴∠EOD=120°,
在四边形BMON中,∠B=60°,∠BMO=∠BNO=90°,
∴∠MON=120°,
∴∠EOM=∠NOD,
在△EOM和△DON中,
$\left\{\begin{array}{l}{∠EOM=∠DDON}\\{OM=ON}\\{∠OME=∠OND}\end{array}\right.$,
∴△EOM≌△DON(ASA),
∴OD=OE.
点评 本题主要考查全等三角形的判定和性质及角平分线的性质,作两边的垂线构造条件证明三角形全等是解题的关键,注意角平分线性质、三角形四边形内角和定理的应用.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
1.下列式子:①a+b=c;②$\root{5}{2}$;③a>0;④a2a,其中,属于代数式的是( )
| A. | ①③ | B. | ②④ | C. | ①③④ | D. | ①②③④ |
7.下列各式从左到右的变形属于因式分解且分解正确的是( )
| A. | (x+1)(x-1)=x2-1 | B. | 2x2-y2=(2x+y)(2x-y) | C. | a2+2a+1=a(a+2)+1 | D. | -a2+4a-4=-(a-2)2 |
 如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点D在AB上,AD=2cm.点E、F同时从点D出发,点E沿DA以1cm每秒的速度向点A运动,到达A点后立即以原速度沿AB向点B匀速运动;点F沿DB以2cm每秒的速度向点B匀速运动,点F运动到点B时停止,点E也随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分面积为S.
如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点D在AB上,AD=2cm.点E、F同时从点D出发,点E沿DA以1cm每秒的速度向点A运动,到达A点后立即以原速度沿AB向点B匀速运动;点F沿DB以2cm每秒的速度向点B匀速运动,点F运动到点B时停止,点E也随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分面积为S.
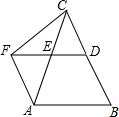 如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC,与DE的延长线相交于点F,连接CF.
如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC,与DE的延长线相交于点F,连接CF.