题目内容
2.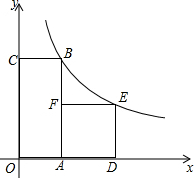 如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半釉上,点F在AB上,点B、E在反比例函数$y=\frac{k}{x}$的图象上OA=1,OC=4.
如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半釉上,点F在AB上,点B、E在反比例函数$y=\frac{k}{x}$的图象上OA=1,OC=4.(1)求反比例函数的解析式;
(2)求正方形ADEF的边长.
分析 (1)根据OA=1,OC=4可得B点坐标(1,4),再把B点坐标代入$y=\frac{k}{x}$可得答案;
(2)设AD=a,则D(a+1,a),根据反比例函数图象上点的坐标特点可得(a+1)a=4,再解即可.
解答 解:(1)∵OA=1,OC=4,
∴B(1,4),
∵B在反比例函数$y=\frac{k}{x}$的图象上,
∴4=$\frac{k}{1}$,
k=4,
∴反比例函数解析式为y=$\frac{4}{x}$;
(2)设AD=a,
∵四边形ADEF是正方形,
∴ED=a,
∴D(a+1,a),
∵E在反比例函数$y=\frac{k}{x}$的图象上,
∴(a+1)a=4,
解得:a1=$\frac{-1+\sqrt{17}}{2}$,a2=$\frac{-1-\sqrt{17}}{2}$(不合题意舍去),
∴正方形ADEF的边长为$\frac{-1+\sqrt{17}}{2}$.
点评 此题主要考查了待定系数法求反比例函数解析式,以及反比例函数图象上点的坐标特点,关键是掌握凡是函数图象经过的点必能满足解析式.

练习册系列答案
相关题目
13.化简:$\frac{\sqrt{2{5}^{2}-{7}^{2}}}{\sqrt{27}}$的结果是( )
| A. | $\frac{8\sqrt{6}}{3}$ | B. | $\frac{8\sqrt{3}}{9}$ | C. | $\frac{4\sqrt{6}}{3}$ | D. | $\frac{8\sqrt{3}}{3}$ |
7.下列各式从左到右的变形属于因式分解且分解正确的是( )
| A. | (x+1)(x-1)=x2-1 | B. | 2x2-y2=(2x+y)(2x-y) | C. | a2+2a+1=a(a+2)+1 | D. | -a2+4a-4=-(a-2)2 |
 如图,将一副三角板的两个直角重合,使点B在EC上,点D在AC上,已知∠A=45°,∠E=30°,则∠BFD的度数是165°.
如图,将一副三角板的两个直角重合,使点B在EC上,点D在AC上,已知∠A=45°,∠E=30°,则∠BFD的度数是165°.