题目内容
1．下列关于x的一元二次方程中，有两个不相等的实数根的方程是（ ）| A． | x2+1=0 | B． | x2-2x+1=0 | C． | x2+x+1=0 | D． | x2+2x-1=0 |
分析 分别计算各选项的判别式△值，然后和0比较大小，再根据一元二次方程根与系数的关系就可以找出符合题意的选项．
解答 解：A、△=-4＜0，方程没有实数根；
B、△＞0，方程有两个相等的实数根；
C、△=1-4=-3＜0，方程没有实数根；
D、△=4+4=8＞0，方程有两个不相等的实数根．
故选D．
点评 本题考查了根的判别式，一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
练习册系列答案
相关题目
观察图中的三角形数阵，则第50行的最后一个数是1275．
12．到三角形三边距离相等的点是（ ）
| A． | 三边垂直平分线的交点 | B． | 三条高所在直线的交点 | ||
| C． | 三条角平分线的交点 | D． | 三条中线的交点 |
16．
如图，AD是∠CAE的平分线，∠B=30°，∠DAE=65°，那么∠ACD等于（ ）
如图，AD是∠CAE的平分线，∠B=30°，∠DAE=65°，那么∠ACD等于（ ）| A． | 60° | B． | 80° | C． | 65°或80° | D． | 100° |
6．下列计算正确的是（ ）
| A． | 6÷3×$\frac{1}{3}$=6 | B． | $\frac{1}{2}$-$\frac{1}{2}$×3=0 | C． | -32-（-23）=1 | D． | （-1$\frac{1}{2}$）2=$\frac{9}{4}$ |
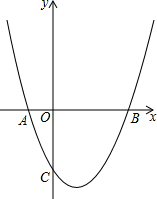已知二次函数y=ax2+bx+c（a≠0）的图象与坐标轴交点的坐标分别为A（-1，0），B（3，0），C（0，-3）．