题目内容
11. 观察图中的三角形数阵,则第50行的最后一个数是1275.
观察图中的三角形数阵,则第50行的最后一个数是1275.
分析 通过观察每行的最后一个数可发现,第一行最后一个数是1,第二行最后一个数是1+2,第三行最后一个数是1+2+3,第四行最后一个数是1+2+3+4,…以此类推,第n行最后一个数是1+2+3+4+5+…+n=$\frac{1}{2}$n(n+1),据此代入计算即可.
解答 解:∵第一行最后一个数是1,
第二行最后一个数是1+2,
第三行最后一个数是1+2+3,
第四行最后一个数是1+2+3+4,
…
第n行最后一个数是1+2+3+4+5+…+n=$\frac{1}{2}$n(n+1),
∴50行的最后一个数是$\frac{1}{2}$×50×51=1275.
故答案为:1275.
点评 此题考查数字的变化规律,找出数字的排列规律与运算规律是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20. 如图,可以看作是由一个等腰直角三角形旋转若干次生成的,则每次旋转的度数是( )
如图,可以看作是由一个等腰直角三角形旋转若干次生成的,则每次旋转的度数是( )
 如图,可以看作是由一个等腰直角三角形旋转若干次生成的,则每次旋转的度数是( )
如图,可以看作是由一个等腰直角三角形旋转若干次生成的,则每次旋转的度数是( )| A. | 45° | B. | 50° | C. | 60° | D. | 72° |
1.下列关于x的一元二次方程中,有两个不相等的实数根的方程是( )
| A. | x2+1=0 | B. | x2-2x+1=0 | C. | x2+x+1=0 | D. | x2+2x-1=0 |
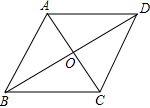 如图,菱形ABCD中,AC、BD交于点O,若AC=4,BD=6,则菱形的面积为12.
如图,菱形ABCD中,AC、BD交于点O,若AC=4,BD=6,则菱形的面积为12. 已知,二次函数y=-$\frac{1}{2}$x2+4x-6的图象与x轴交于A、B两点(A点B点左侧),与y轴交于C点.
已知,二次函数y=-$\frac{1}{2}$x2+4x-6的图象与x轴交于A、B两点(A点B点左侧),与y轴交于C点.