题目内容
11.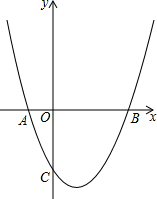 已知二次函数y=ax2+bx+c(a≠0)的图象与坐标轴交点的坐标分别为A(-1,0),B(3,0),C(0,-3).
已知二次函数y=ax2+bx+c(a≠0)的图象与坐标轴交点的坐标分别为A(-1,0),B(3,0),C(0,-3).(1)求此函数的解析式;
(2)求抛物线的开口方向、对称轴及顶点坐标;
(3)根据图象直接写出y<0时x的取值范围.
分析 (1)设抛物线的解析式为y=a(x-x1)(x-x2),再把A(-1,0),B(3,0),C(0,-3)代入即可得出此函数的解析式;
(2)根据a的符号判断抛物线的开口方向、由顶点公式得出对称轴及顶点坐标;
(3)由题意把函数转化为不等式,得x2-2x-3>0,从而求出x的取值范围.
解答 解:(1)设抛物线的解析式为y=a(x-x1)(x-x2),
把A(-1,0),B(3,0),C(0,-3)代入得a(0+1)(0-3)=-3,
解得a=1,
∴此函数的解析式y=(x+1)(x-3)即y=x2-2x-3;
(2)∵a=1>0,
∴抛物线的开口向上,
对称轴为直线x=-$\frac{b}{2a}$=1,
$\frac{4ac-{b}^{2}}{4a}$=$\frac{-12-4}{4}$=-4,
顶点坐标(1,-4);
(3)∵y<0,即图象在x轴的下方,
∴由图象可知:当-1<x<3时,y<0.
点评 本题考查了二次函数的性质,以及用待定系数法求二次函数的解析式,求抛物线的顶点坐标的方法,是中考的常见题型.

练习册系列答案
相关题目
1.下列关于x的一元二次方程中,有两个不相等的实数根的方程是( )
| A. | x2+1=0 | B. | x2-2x+1=0 | C. | x2+x+1=0 | D. | x2+2x-1=0 |
2.下列说法:
(1)所有的黄金矩形都相似;
(2)在同圆或等圆中,相等的弦所对的弧相等;
(3)方程2x(x-1)=x-1的解为x=$\frac{1}{2}$;
(4)平面内任意3个点确定一个圆;
其中正确的说法的个数是( )
(1)所有的黄金矩形都相似;
(2)在同圆或等圆中,相等的弦所对的弧相等;
(3)方程2x(x-1)=x-1的解为x=$\frac{1}{2}$;
(4)平面内任意3个点确定一个圆;
其中正确的说法的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.在△ABC中,∠A=20°,∠B=60°,则∠C的度数( )
| A. | 80° | B. | 90° | C. | 20° | D. | 100° |
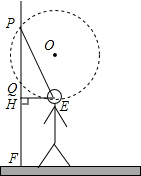 如图,墙壁上的展品最高点与地面的距离PF=3.2m,最低点与地面的距离QF=2m,观赏者的眼睛E距地面1.6m,经验表明,当水平视线EH与过P,Q,E点的圆相切于点E时,视角最大,站在此处观赏最理想,求此时点E到墙壁的距离EH.
如图,墙壁上的展品最高点与地面的距离PF=3.2m,最低点与地面的距离QF=2m,观赏者的眼睛E距地面1.6m,经验表明,当水平视线EH与过P,Q,E点的圆相切于点E时,视角最大,站在此处观赏最理想,求此时点E到墙壁的距离EH.