题目内容
7. 情景再现
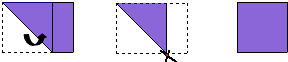
情景再现通过“活动 思考”一节的学习,小红知道了:把一张长方形纸片按下图要求折叠、裁剪、展开,可以得到由长方形裁剪出的一个最大正方形.
操作探究
聪明的小红在学习了这一个知识后给出了一个“可裁长方形”的定义:当相邻两边长分别为1,a(a>1)的长方形通过上述方法裁剪掉一个最大的正方形后,再在剩下的部分裁剪出一个最大的正方形,如此反复,最后剩下的部分也是一个正方形,像这样一类长方形称为可裁长方形.并进行了以下探索:
(1)当一个可裁长方形只经过一次裁剪就可以得到全部正方形,则a的值为2;
(2)当一个可裁长方形只经过两次裁剪就可以得到全部正方形,则所有符合条件的a的值为1.5或3;
(3)当一个可裁长方形只经过三次裁剪就可以得到全部正方形,画出所有符合条件可裁长方形,标注出裁剪线,并在对应的图形下方写出a的值.
方法迁移
取一个自然数,若它是奇数,则乘以3加上1;若它是偶数,则除以2,按此规则经过若干步的计算最终可得到1.这个结论在数学上还没有得到证明.但举例验证都是正确的.例如:取自然数5.最少经过下面5步运算可得1,
即:5$\stackrel{×3+1}{→}$16$\stackrel{÷2}{→}$8$\stackrel{÷2}{→}$4$\stackrel{÷2}{→}$2$\stackrel{÷2}{→}$1,
(1)自然数12最少经过9步运算可得到1
(2)如果自然数m最少经过7步运算可得到1,则所有符合条件的m的值为128、21、20、3.
分析 操作探究(1)根据操作的方法可得a=2;
(2)当一个可裁长方形只经过两次裁剪就可以得到全部正方形,则所有符合条件的a的值为3个1或1为2个(a-1);
(3)结合(1)、(2)题作出图形;
方法迁移(1)利用列举法,尝试最小的几个非0自然数,再结合“自然数5.最少经过5步运算可得1”,即可得出结论;
(2)首先根据题意,应用逆推法,用1乘以2,得到2;用2乘以2,得到4;用4乘以2,得到8;用8乘以2,得到16;然后分类讨论,判断出所有符合条件的m的值为多少即可.
解答 解:操作探究:
(1)当一个可裁长方形只经过一次裁剪就可以得到全部正方形,则a的值为2个1,
故答案为:2;
(2)当一个可裁长方形只经过两次裁剪就可以得到全部正方形,则所有符合条件的a的值为3个1或1为2个(a-1),
故答案为:1.5或3;
(3)当一个可裁长方形只经过三次裁剪就可以得到全部正方形,画出符合条件可裁长方形如图: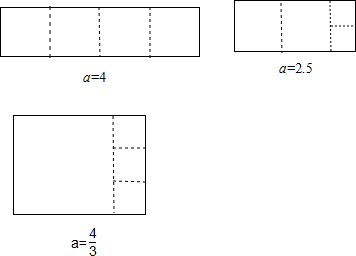
方法迁移:
(1)12$\stackrel{÷2}{→}$6$\stackrel{÷2}{→}$3$\stackrel{×3+1}{→}$10$\stackrel{÷2}{→}$5$\stackrel{×3+1}{→}$16$\stackrel{÷2}{→}$8$\stackrel{÷2}{→}$4$\stackrel{÷2}{→}$2$\stackrel{÷2}{→}$1,
自然数12最少经过9步运算可得到1,
故答案为:9;
(2)根据分析,可得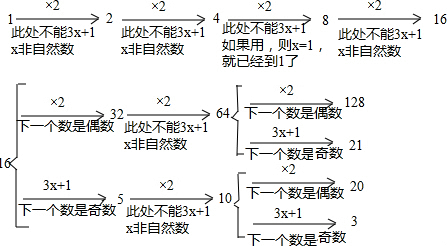
则所有符合条件的m的值为:128、21、20、3.
故答案为:128、21、20、3.
点评 (1)此题主要考查了探寻数列规律问题,考查了逆推法的应用,注意观察总结出规律,并能正确的应用规律.
(2)此题还考查了推理和论证问题,要熟练掌握,解答此题的关键是要明确:①演绎推理是从一般规律出发,运用逻辑证明或数学运算,得出特殊事实应遵循的规律,即从一般到特殊.②归纳推理就是从许多个别的事物中概括出一般性概念、原则或结论,即从特殊到一般.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{3}$ |

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,
如图,
 如图所示,二次函数y1=a(x-b)2的图象与直线y2=kx+b交于A(0,-1)、B(1,0)两点.
如图所示,二次函数y1=a(x-b)2的图象与直线y2=kx+b交于A(0,-1)、B(1,0)两点.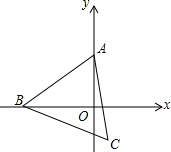 如图,在直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持△ABC是等边三角形(点A、B、C按逆时针排列),当点B运动到原点O处时,则点C的坐标是($\sqrt{3}$,1).随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的解析式是y=$\sqrt{3}$x-2.
如图,在直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持△ABC是等边三角形(点A、B、C按逆时针排列),当点B运动到原点O处时,则点C的坐标是($\sqrt{3}$,1).随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的解析式是y=$\sqrt{3}$x-2.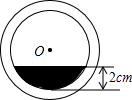 将一盛有不足半杯水的圆柱形玻璃水拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是($\frac{16}{3}$π-4$\sqrt{3}$)cm2.
将一盛有不足半杯水的圆柱形玻璃水拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是($\frac{16}{3}$π-4$\sqrt{3}$)cm2.