题目内容
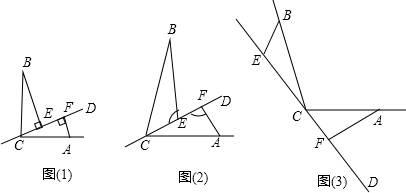
15.已知C,D过∠BCA顶点的一条直线,CA=CB,E,F是直线CD上的两点,且∠BEC=∠CFA.(1)如图(1),若∠BCA=90°,∠BEC=∠CFA=90°,则BE==CF(填“>”、“<”或“=”)
(2)如图(2),∠BCA+∠BEC=180°,则(1)中的结论是否成立?为什么?
(3)如图(3),若∠BEC=∠CFA=∠BCA,则线段EF,BE,AF之间有何数量关系?说明理由.
分析 (1)根据三角形内角和定理和直角求出∠CBE=∠ACF,利用AAS即可证明三角形BCE与三角形CAF全等,根据全等三角形的对应边相等得到BE=CF
(2)先证明∠CBE=∠ACF,利用AAS即可证明三角形BCE与三角形CAF全等,根据全等三角形的对应边相等得到BE=CF.
(3)结论:EF=AF+BE,首先证明∠CBE=∠ACF,利用AAS即可证明三角形BCE与三角形CAF全等,根据全等三角形的对应边相等得到BE=CF,CE=AF,即可得出EF=AF+BE
解答 (1)解:如图1中,∵∠BCA=∠BEC=∠CFA=90°,
∴∠BCE+∠ACF=90°,∠ACF+∠CAF=90°,
∴∠BCE=∠CAF,
在△BCE和△CAF中,
$\left\{\begin{array}{l}{∠CEB=∠CFA}\\{∠BCE=∠CAF}\\{BC=AC}\end{array}\right.$,
∴△BCE≌△CAF(AAS),
∴BE=CF,CE=AF,
∴EF=|CF-CE|=|BE-AF|,
故答案为=.
(2)成立.理由如下,
证明:如图2中,∵∠BCA+∠BEC=180°,∠BCE+∠BEF=180°,
∴∠BCA=∠BEF,
∴∠ACF+∠BCE=∠BCE+∠CBE,
∴∠CBE=∠ACF,
在△BCE和△CAF中,
$\left\{\begin{array}{l}{∠CEB=∠CFA}\\{∠BCE=∠CAF}\\{BC=AC}\end{array}\right.$,
∴△BCE≌△CAF(AAS),
∴BE=CF.
(3)结论:EF=AF+BE,理由如下.
证明:如图3中,∵∠BCF=∠BEC+∠CBE=∠BCA+∠ACF
∵∠BEC=∠BCA,
∴∠CBE=∠ACF,
在△BCE和△CAF中,
$\left\{\begin{array}{l}{∠CEB=∠CFA}\\{∠BCE=∠CAF}\\{BC=AC}\end{array}\right.$,
∴△BCE≌△CAF(AAS),
∴BE=CF,CE=AF,
∴EF=AF+BE.
点评 本题考查了全等三角形的性质和判定,三角形的内角和定理的应用,此题是一道比较复杂的题目,综合性比较强,本题考查了从特殊到一般的过程,考查了学生的分析能力和推理能力,属于中考常考题型.

 阅读快车系列答案
阅读快车系列答案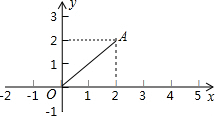 如图,点A的坐标为(2,2),若点P在坐标轴上,且△APO为等腰三角形,则满足条件的点P个数是( )
如图,点A的坐标为(2,2),若点P在坐标轴上,且△APO为等腰三角形,则满足条件的点P个数是( )| A. | 4个 | B. | 6个 | C. | 7个 | D. | 8个 |
 如图,在△ABC中,AB=CA,∠CAB=90°,F为BA延长线上一点,点E在线段AC上,
如图,在△ABC中,AB=CA,∠CAB=90°,F为BA延长线上一点,点E在线段AC上,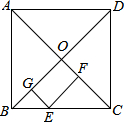 在正方形ABCD中,E为BC边上一点,EF⊥AC,垂足为F,EG⊥BD,垂足为G,BD=6,则EF+EG为3.
在正方形ABCD中,E为BC边上一点,EF⊥AC,垂足为F,EG⊥BD,垂足为G,BD=6,则EF+EG为3. 情景再现
情景再现 如图:(1)∠1和∠5是直线AB与直线DC被直线BE所截形成的同位角,
如图:(1)∠1和∠5是直线AB与直线DC被直线BE所截形成的同位角,