题目内容
12. 如图所示,二次函数y1=a(x-b)2的图象与直线y2=kx+b交于A(0,-1)、B(1,0)两点.
如图所示,二次函数y1=a(x-b)2的图象与直线y2=kx+b交于A(0,-1)、B(1,0)两点.(1)确定二次函数的解析式;
(2)当y1<y2,y1=y2,y1>y2时,根据图象分别确定自变量x的取值范围.
分析 (1)把点A、B的坐标分别代入函数解析式,列出关于a、b的方程组,通过解该方程组即可求得它们的值;
(2)根据当y1<y2时,y1的图象在y2的图象下面,y1=y2时,x的值就是交点的横坐标,y1>y2时,y1的图象在y2的图象上面,由此可以解决问题.
解答 解:(1)把A(0,-1)、B(1,0)分别代入y2=kx+b,得$\left\{\begin{array}{l}{b=-1}\\{k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$,
所以y1=a(x-1)2.
(2)由图象可知:
①当x<0或x>1时,y1<y2,
②当x=0或1时,y1=y2,
③当0<x<1时,y1>y2.
点评 本题考查二次函数的解析式的求法,掌握用待定系数法求解析式,解题的关键是能够利用函数图象根据要求确定自变量取值范围,属于中考常考题型.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
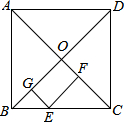 在正方形ABCD中,E为BC边上一点,EF⊥AC,垂足为F,EG⊥BD,垂足为G,BD=6,则EF+EG为3.
在正方形ABCD中,E为BC边上一点,EF⊥AC,垂足为F,EG⊥BD,垂足为G,BD=6,则EF+EG为3. 情景再现
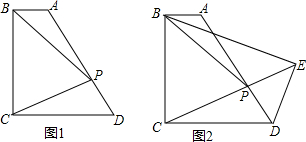
情景再现 如图:(1)∠1和∠5是直线AB与直线DC被直线BE所截形成的同位角,
如图:(1)∠1和∠5是直线AB与直线DC被直线BE所截形成的同位角, 如图,AC⊥AE,BD⊥BF,∠1=∠2,图中有那几组平行线,并说明理由.
如图,AC⊥AE,BD⊥BF,∠1=∠2,图中有那几组平行线,并说明理由.