题目内容
10.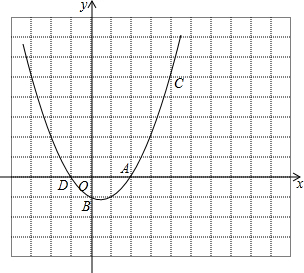 如图,
如图,(1)求二次函数的解析式.
(2)设二次函数与x轴的另一个交点为D,并在抛物线的对称轴上找一点P,使三角形PBD的周长最小,求出点D和点P的坐标.
(3)在直线CD下方的抛物线上是否存在一点E,使得△DCE的面积最大,若有求出点E坐标及面积的最大值.
分析 (1)根据待定系数法,可得函数解析式;
(2)根据线段垂直平分线上的点到线段两端点的距离相等,可得P在BA上,根据待定系数法,可得BA的解析式,根据自变量与函数值的对应关系,可得P点坐标,可得D点坐标;
(3)根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得EF的长,根据面积的和差,可得二次函数,根据二次函数的性质,可得最大面积,根据自变量与函数值的对应关系,可得答案.
解答 解:(1)设二次函数的解析式为y=ax2+bx+c,将A、B、C点坐标代入函数解析式,得
$\left\{\begin{array}{l}{4a+2b+c=0}\\{16a+4b+c=0}\\{c=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{1}{2}}\\{c=-1}\end{array}\right.$.
故抛物线的解析式为y=$\frac{1}{2}$x2-$\frac{1}{2}$x-1;
(2)如图1, ,
,
当y=0时,$\frac{1}{2}$x2-$\frac{1}{2}$x-1=0.解得x=-1,x=2(不符合题意,舍),即D点坐标为(-1,0);
y=$\frac{1}{2}$x2-$\frac{1}{2}$x-1=$\frac{1}{2}$(x-$\frac{1}{2}$)2-$\frac{9}{8}$,抛物线的对称轴为x=$\frac{1}{2}$.
连接BA交 对称轴于P点,设BA的解析式为y=kx+b,将B、A点坐标代入,得
$\left\{\begin{array}{l}{2k+b=0}\\{b=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-1}\end{array}\right.$.
BA的解析式为y=$\frac{1}{2}$x-1.
当x=$\frac{1}{2}$时,y=$\frac{1}{2}$×$\frac{1}{2}$-1=-$\frac{3}{4}$
即P($\frac{1}{2}$,-$\frac{3}{4}$);
(3)如图2,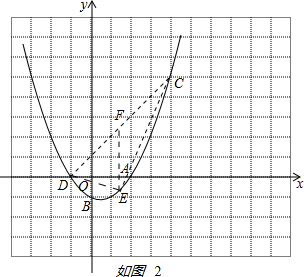 ,
,
设CD的解析式为y=kx+b,将C、D点坐标代入函数解析式,得
$\left\{\begin{array}{l}{4k+b=5}\\{-k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$.
CD的解析式为y=x+1,F在CD上,E在抛物线上,
设E点坐标为(m,$\frac{1}{2}$m2-$\frac{1}{2}$m-1),F点坐标为(m,m+1).
FE=m+1-($\frac{1}{2}$m2-$\frac{1}{2}$m-1)=-$\frac{1}{2}$m2+$\frac{3}{2}$m+2,
S△DCE=$\frac{1}{2}$EF•(xC-xD)
=$\frac{1}{2}$×(-$\frac{1}{2}$m2+$\frac{3}{2}$m+2)×[4-(-1)]
=$\frac{5}{2}$[-$\frac{1}{2}$(m-$\frac{3}{2}$)2+$\frac{25}{8}$]
当m=$\frac{3}{2}$时,S△DCE最大=$\frac{125}{16}$,
当m=$\frac{3}{2}$时,y=$\frac{1}{2}$m2-$\frac{1}{2}$m-1=-$\frac{5}{8}$,
即E点坐标为($\frac{3}{2}$,-$\frac{5}{8}$).
点评 本题考察了二次函数综合题,利用待定系数法求函数解析式;利用线段垂直平分线上的点到线段两端点的距离相等得出P在BA上是解题关键;利用面积的和差得出二次函数是解题关键.

 智慧小复习系列答案
智慧小复习系列答案| A. | 0 | B. | $\sqrt{3}$ | C. | 2 | D. | -3 |
 如图,抛物线y=ax2+bx+c与y轴相交于点(0,$\frac{5}{2}$),与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线A、B两点间部分上的一动点(不与点A、B重合),直线CD∥y轴,交直线AB于C,连接AD、BD.
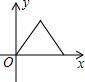
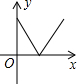
如图,抛物线y=ax2+bx+c与y轴相交于点(0,$\frac{5}{2}$),与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线A、B两点间部分上的一动点(不与点A、B重合),直线CD∥y轴,交直线AB于C,连接AD、BD.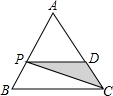 如图,P为等边三角形ABC中AB边上的动点,沿A→B的方向运动,到达点B时停止,过P作PD∥BC.设AP=x,△PDC的面积为y,则y关于x的函数图象大致为( )
如图,P为等边三角形ABC中AB边上的动点,沿A→B的方向运动,到达点B时停止,过P作PD∥BC.设AP=x,△PDC的面积为y,则y关于x的函数图象大致为( )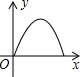
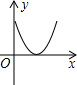
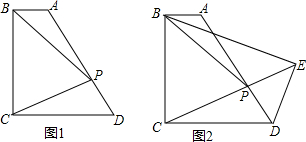
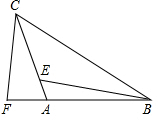 如图,在△ABC中,AB=CA,∠CAB=90°,F为BA延长线上一点,点E在线段AC上,
如图,在△ABC中,AB=CA,∠CAB=90°,F为BA延长线上一点,点E在线段AC上, 情景再现
情景再现