题目内容
16.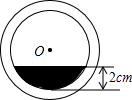 将一盛有不足半杯水的圆柱形玻璃水拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是($\frac{16}{3}$π-4$\sqrt{3}$)cm2.
将一盛有不足半杯水的圆柱形玻璃水拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是($\frac{16}{3}$π-4$\sqrt{3}$)cm2.
分析 作OD⊥AB于C,交小⊙O于D,则CD=2,由垂径定理可知AC=CB,利用正弦函数求得∠OAC=30°,进而求得∠AOC=120°,利用勾股定理即可求出AB的值,从而利用S扇形-S△AOB求得杯底有水部分的面积.
解答 解:作OD⊥AB于C,交小⊙O于D,则CD=2,AC=BC,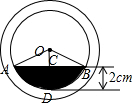
∵OA=OD=4,CD=2,
∴OC=2,
在RT△AOC中,sin∠OAC=$\frac{OC}{OA}$=$\frac{1}{2}$,
∴∠OAC=30°,
∴∠AOB=120°,
AC=$\sqrt{O{A}^{2}-O{C}^{2}}$=2$\sqrt{3}$,
∴AB=4$\sqrt{3}$,
∴杯底有水部分的面积=S扇形-S△AOB=$\frac{120π×{4}^{2}}{360}$-$\frac{1}{2}$×4$\sqrt{3}$×2=($\frac{16}{3}$π-4$\sqrt{3}$)cm2
故答案为($\frac{16}{3}$π-4$\sqrt{3}$)cm2.
点评 本题考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.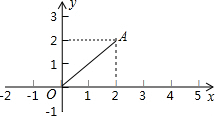 如图,点A的坐标为(2,2),若点P在坐标轴上,且△APO为等腰三角形,则满足条件的点P个数是( )
如图,点A的坐标为(2,2),若点P在坐标轴上,且△APO为等腰三角形,则满足条件的点P个数是( )
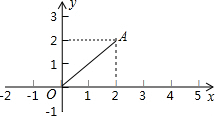 如图,点A的坐标为(2,2),若点P在坐标轴上,且△APO为等腰三角形,则满足条件的点P个数是( )
如图,点A的坐标为(2,2),若点P在坐标轴上,且△APO为等腰三角形,则满足条件的点P个数是( )| A. | 4个 | B. | 6个 | C. | 7个 | D. | 8个 |
6. 有理数a和b在数轴上的位置如图所示,则下列关系正确的是( )
有理数a和b在数轴上的位置如图所示,则下列关系正确的是( )
 有理数a和b在数轴上的位置如图所示,则下列关系正确的是( )
有理数a和b在数轴上的位置如图所示,则下列关系正确的是( )| A. | a+b<0 | B. | ab>0 | C. | -a<b<0 | D. | -a<-b<0 |
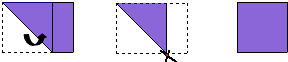 情景再现
情景再现 如图:(1)∠1和∠5是直线AB与直线DC被直线BE所截形成的同位角,
如图:(1)∠1和∠5是直线AB与直线DC被直线BE所截形成的同位角,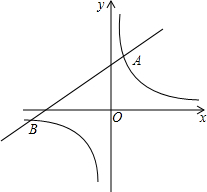 如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=2x+b的图象相交于点A(1,4)和点B(n,-2).
如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=2x+b的图象相交于点A(1,4)和点B(n,-2). 如图,AC⊥AE,BD⊥BF,∠1=∠2,图中有那几组平行线,并说明理由.
如图,AC⊥AE,BD⊥BF,∠1=∠2,图中有那几组平行线,并说明理由.