题目内容

17．抛物线y=x2-2x-3与y轴的交点坐标是（0，-3）．

分析 由于抛物线与y轴的交点的横坐标为0，把x=0当然抛物线的解析式中即可求出纵坐标．

解答 解：∵抛物线y=x2-2x-3，
∴当x=0时，y=-3，
∴抛物线y=x2-2x-3与y轴的交点坐标是（0，-3）．
故答案为：（0，-3）．

点评 本题考查了二次函数图象上点的坐标特征，比较简单，掌握y轴上点的横坐标为0是解题的关键．

练习册系列答案
相关题目
7．情景再现
通过“活动 思考”一节的学习，小红知道了：把一张长方形纸片按下图要求折叠、裁剪、展开，可以得到由长方形裁剪出的一个最大正方形．
操作探究
聪明的小红在学习了这一个知识后给出了一个“可裁长方形”的定义：当相邻两边长分别为1，a（a＞1）的长方形通过上述方法裁剪掉一个最大的正方形后，再在剩下的部分裁剪出一个最大的正方形，如此反复，最后剩下的部分也是一个正方形，像这样一类长方形称为可裁长方形．并进行了以下探索：
（1）当一个可裁长方形只经过一次裁剪就可以得到全部正方形，则a的值为2；
（2）当一个可裁长方形只经过两次裁剪就可以得到全部正方形，则所有符合条件的a的值为1.5或3；
（3）当一个可裁长方形只经过三次裁剪就可以得到全部正方形，画出所有符合条件可裁长方形，标注出裁剪线，并在对应的图形下方写出a的值．
方法迁移
取一个自然数，若它是奇数，则乘以3加上1；若它是偶数，则除以2，按此规则经过若干步的计算最终可得到1．这个结论在数学上还没有得到证明．但举例验证都是正确的．例如：取自然数5．最少经过下面5步运算可得1，
即：5$\stackrel{×3+1}{→}$16$\stackrel{÷2}{→}$8$\stackrel{÷2}{→}$4$\stackrel{÷2}{→}$2$\stackrel{÷2}{→}$1，
（1）自然数12最少经过9步运算可得到1
（2）如果自然数m最少经过7步运算可得到1，则所有符合条件的m的值为128、21、20、3．
8．若-5x3ym与6xny2是同类项，则m+n=5．
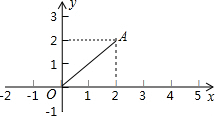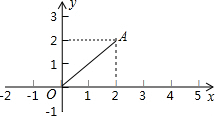5．如图，点A的坐标为（2，2），若点P在坐标轴上，且△APO为等腰三角形，则满足条件的点P个数是（　　）
A．4个B．6个C．7个D．8个
12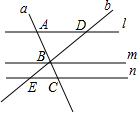．如图，已知直线l∥m∥n，直线a分别与l，m，n交于点A，B，C，过点B作直线b交直线l，n于点D，E，若AB=2，BC=1，BD=3，则BE的长为（　　）
A．4B．2C．$\frac{2}{3}$D．$\frac{3}{2}$
2．计算：sin30°-tan60°tan30°+2cos230°．
9．化简：$\sqrt{32}$×$\sqrt{2}$=8．
6．有理数a和b在数轴上的位置如图所示，则下列关系正确的是（　　）
A．a+b＜0B．ab＞0C．-a＜b＜0D．-a＜-b＜0
7．下列计算正确的是（　　）
A．x2+x3=2x5B．（-x3）2=-x6C．x6÷x3=x3D．x2•x3=x6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网