Question

19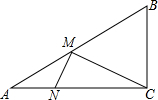．如图，在△ABC中，∠ACB=90°，AC=8，BC=6，动点M从A点出发，以每秒2个单位长度的速度向B点运动；动点N也从A点同时出发，以每秒1个单位长度的速度向C点运动．当M，N有一点到达终点时，两点都停止运动．
（1）AB的长为10；
（2）△MCN的面积的最大值是$\frac{48}{5}$．

Answer 1

分析 （1）利用勾股定理直接计算即可求出AB的长；
（2）过点M，作MD⊥AC于点D，首先求出△MCN面积的表达式，利用二次函数的性质，求出△MCN面积最大值．

解答 解：（1）在△ABC中，∠ACB=90°，AC=8，BC=6，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10．
故答案为10；
（2）过点M，作MD⊥AC于点D，
∵BC⊥AC，
∴MD∥BC，
∴△AMD∽△ABC，
∴ND：BC=AM：AB，
∵动点M从A点出发，以每秒2个单位长度的速度向B点运动；动点N也从A点同时出发，以每秒1个单位长度的速度向C点运动，
∴AM=2t，NC=AC-AN=8-t，
∴$\frac{MD}{6}=\frac{2t}{10}$，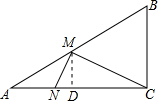
∴MD=$\frac{6}{5}$t，
∴S_△MNC=$\frac{1}{2}$NC•MD=$\frac{1}{2}$（8-t）•$\frac{6}{5}$t=-$\frac{3}{5}$（t-4）²+$\frac{48}{5}$，
∵当M，N有一点到达终点时，两点都停止运动，
∴0≤t≤5，
∴△MCN的面积的最大值是$\frac{48}{5}$．
故答案为$\frac{48}{5}$．

点评 本题考查了相似三角形的判定和性质、勾股定理的运用以及二次函数的最值等知识点．试题难度不大，需要注意的是（2）问中，自变量取值区间上求最大值，而不能机械地套用公式．