题目内容
9.一圆柱的侧面展开图是边长分别为6和8的长方形,則该圆柱的底面积是( )| A. | 3π或4π | B. | $\frac{3}{π}$或$\frac{4}{π}$ | C. | $\frac{6}{π}$或$\frac{8}{π}$ | D. | $\frac{9}{π}$或$\frac{16}{π}$ |
分析 分两种情况:①底面周长为6,②底面周长为8,根据圆的周长公式求得该圆柱的底面半径,再根据圆的面积公式可求该圆柱的底面积.
解答 解:分两种情况:
①底面周长为6,
该圆柱的底面积是π×($\frac{6}{2π}$)2=$\frac{9}{π}$;
②底面周长为8,
该圆柱的底面积是π×($\frac{8}{2π}$)2=$\frac{16}{π}$;
综上所述,该圆柱的底面积是$\frac{9}{π}$或$\frac{16}{π}$.
故选:D.
点评 考查了几何体的展开图,本题关键是求得该圆柱的底面半径,注意分类思想的应用.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
17.某商店对于某个商品的销售量与获利做了统计,得到下表:
若获利是销售量的二次函数,那么,该商店获利的最大值是( )
| 销售量(件) | 100 | 200 | 300 |
| 获利(万元) | 7 | 9 | 9 |
| A. | 9万元 | B. | 9.25万元 | C. | 9.5万元 | D. | 10万元 |
14. 如图,已知:B是线段AD上的一点,△ABC、△BDE均为等边三角形,AE交BC于P,CD交BE于Q.则下列结论成立的有( )
如图,已知:B是线段AD上的一点,△ABC、△BDE均为等边三角形,AE交BC于P,CD交BE于Q.则下列结论成立的有( )
(1)AE=CD;(2)BP=BQ;(3)PQ∥AD;(4)CQ=CA;(5)EP=QD.
 如图,已知:B是线段AD上的一点,△ABC、△BDE均为等边三角形,AE交BC于P,CD交BE于Q.则下列结论成立的有( )
如图,已知:B是线段AD上的一点,△ABC、△BDE均为等边三角形,AE交BC于P,CD交BE于Q.则下列结论成立的有( )(1)AE=CD;(2)BP=BQ;(3)PQ∥AD;(4)CQ=CA;(5)EP=QD.
| A. | 5个 | B. | 2个 | C. | 3个 | D. | 4个 |
18. 如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4$\sqrt{2}$,则△BEF的面积是( )
如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4$\sqrt{2}$,则△BEF的面积是( )
 如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4$\sqrt{2}$,则△BEF的面积是( )
如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4$\sqrt{2}$,则△BEF的面积是( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
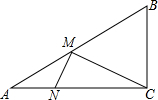 如图,在△ABC中,∠ACB=90°,AC=8,BC=6,动点M从A点出发,以每秒2个单位长度的速度向B点运动;动点N也从A点同时出发,以每秒1个单位长度的速度向C点运动.当M,N有一点到达终点时,两点都停止运动.
如图,在△ABC中,∠ACB=90°,AC=8,BC=6,动点M从A点出发,以每秒2个单位长度的速度向B点运动;动点N也从A点同时出发,以每秒1个单位长度的速度向C点运动.当M,N有一点到达终点时,两点都停止运动. 如图是一个棱长为10cm的正方体盒子,现需从底部A点处起,沿盒子的三个表面到顶部的B点处张贴一条彩色纸带(纸带的宽度忽略不计),则所需纸带的最短长度是=10$\sqrt{10}$cm.
如图是一个棱长为10cm的正方体盒子,现需从底部A点处起,沿盒子的三个表面到顶部的B点处张贴一条彩色纸带(纸带的宽度忽略不计),则所需纸带的最短长度是=10$\sqrt{10}$cm.