题目内容
8.抛物线y=ax2+3与x轴的两个交点分别为(m,0)和(n,0),则当x=m+n时,y的值为( )| A. | 0 | B. | 2 | C. | 3 | D. | 6 |
分析 利用抛物线与x轴的交点问题,可判断m、n为一元二次方程ax2+3=0的两根,利用根与系数的关系得到m+n=0,然后计算自变量为0所对应的函数值即可.
解答 解:∵抛物线y=ax2+3与x轴的两个交点分别为(m,0)和(n,0),
∴m、n为一元二次方程ax2+3=0的两根,
∴m+n=0,
当x=m+n=0时,y=ax2+3=3.
故选C.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.

练习册系列答案
相关题目
17.某商店对于某个商品的销售量与获利做了统计,得到下表:
若获利是销售量的二次函数,那么,该商店获利的最大值是( )
| 销售量(件) | 100 | 200 | 300 |
| 获利(万元) | 7 | 9 | 9 |
| A. | 9万元 | B. | 9.25万元 | C. | 9.5万元 | D. | 10万元 |
18. 如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4$\sqrt{2}$,则△BEF的面积是( )
如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4$\sqrt{2}$,则△BEF的面积是( )
 如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4$\sqrt{2}$,则△BEF的面积是( )
如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4$\sqrt{2}$,则△BEF的面积是( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
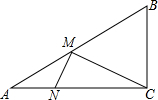 如图,在△ABC中,∠ACB=90°,AC=8,BC=6,动点M从A点出发,以每秒2个单位长度的速度向B点运动;动点N也从A点同时出发,以每秒1个单位长度的速度向C点运动.当M,N有一点到达终点时,两点都停止运动.
如图,在△ABC中,∠ACB=90°,AC=8,BC=6,动点M从A点出发,以每秒2个单位长度的速度向B点运动;动点N也从A点同时出发,以每秒1个单位长度的速度向C点运动.当M,N有一点到达终点时,两点都停止运动.


