题目内容
11. 如图,AB是⊙O的一条弦,C,D是⊙O上的两个动点,且在AB弦的异侧,连接CD.
如图,AB是⊙O的一条弦,C,D是⊙O上的两个动点,且在AB弦的异侧,连接CD.(1)已知AC=BC,AB平分∠CBD,求证:AB=CD;
(2)已知∠ADB=45°,⊙O的半径为1,求四边形ACBD面积的最大值.
分析 (1)证$\widehat{AC}=\widehat{BC}$=$\widehat{AD}$,即可得$\widehat{DAC}=\widehat{ACB}$,从而得证;
(2)由S四边形ABCD=S△ADB+S△ACB,设△ADB和△ACB的公共边AB上的高为h1、h2,则h1+h2的最大值为⊙O的直径,即当点C在劣弧AB的中点、点D在优弧AB的中点时,四边形ABCD的面积最大,根据∠ADB=45°知∠AOB=90°,根据AO=BO=1得AB=$\sqrt{2}$,由S四边形ABCD=$\frac{1}{2}$AB(h1+h2)可得答案.
解答 解:(1)∵AC=BC,
∴$\widehat{AC}=\widehat{BC}$,
∵AB平分∠CBD,
∴∠CBA=∠DBA,
∴$\widehat{AC}=\widehat{AD}$,
∴$\widehat{DAC}=\widehat{ACB}$,
∴AB=CD;
(2)∵S四边形ABCD=S△ADB+S△ACB,
设△ADB和△ACB的公共边AB上的高为h1、h2,则h1+h2的最大值为⊙O的直径,
即当点C在劣弧AB的中点、点D在优弧AB的中点时,四边形ABCD的面积最大,
如图,连接OA、OB,
∵∠ADB=45°,
∴∠AOB=90°,
∵AO=BO=1,
∴AB=$\sqrt{2}$,
∴S四边形ABCD=$\frac{1}{2}$AB(h1+h2)=$\frac{1}{2}$×$\sqrt{2}$×2=$\sqrt{2}$.
点评 本题主要考查圆周角定理、角平分线的性质、勾股定理等知识点,由△ADB和△ACB的公共边AB上的高为h1、h2,则h1+h2的最大值为⊙O的直径时,四边形ABCD的面积最大是解题的关键.

练习册系列答案
相关题目
3.某学校为选拔数学能力突出的学生参加中学生数学竞赛,组织了多次测试,其中甲乙两位同学成绩较为优秀,他们在六次赛前测试中的成绩(单位:分)如下表所示.
如果根据这六次成绩选拔其中一人参加比赛,你认为哪一位比较合适?为什么?
| 甲 | 80 | 75 | 90 | 64 | 88 | 95 |
| 乙 | 84 | 80 | 88 | 76 | 79 | 85 |
1.下面图形中不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
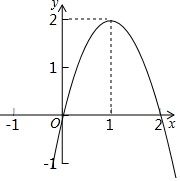 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题.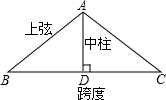 如图,厂房屋顶人字架(等腰三角形)的跨度为20m,∠B=37°,求中柱AD(D为底边中点)和上弦AB的长(参考数据:cos37°≈0.6)
如图,厂房屋顶人字架(等腰三角形)的跨度为20m,∠B=37°,求中柱AD(D为底边中点)和上弦AB的长(参考数据:cos37°≈0.6)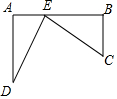 如图,铁路上A,B两站(视为线上两点)相距25千米,C,D为铁路同旁两个村庄(视为两点),DA⊥AB于A点,CB⊥AB于B点,DA=15千米,CB=10千米,现在要在铁路AB上修一个土特品回购站E,使C,D两村庄到E站的距离相等,则E站应建在距A站10千米处.
如图,铁路上A,B两站(视为线上两点)相距25千米,C,D为铁路同旁两个村庄(视为两点),DA⊥AB于A点,CB⊥AB于B点,DA=15千米,CB=10千米,现在要在铁路AB上修一个土特品回购站E,使C,D两村庄到E站的距离相等,则E站应建在距A站10千米处.