题目内容
17. 如图,四边形ABCD是正方形,以B点为圆心,BD的长为半径画弧交BC延长线于点E,以DE为边作正方形DEFG,作FH⊥BE交BE的延长线于点H,连接AE、CG,则下列结论中正确的有( )
如图,四边形ABCD是正方形,以B点为圆心,BD的长为半径画弧交BC延长线于点E,以DE为边作正方形DEFG,作FH⊥BE交BE的延长线于点H,连接AE、CG,则下列结论中正确的有( )①∠CDE=22.5°;②S正方形DEFG-S正方形ABCD=FH2;③AE⊥CG;④DC2=CP•CG;⑤S△DCE:S△BCD=$\sqrt{2}$-1.
| A. | ①②③④⑤ | B. | ①②③④ | C. | ①②③ | D. | ①②③⑤ |
分析 ①正确.根据等腰三角形的性质求出∠BDE=67.5°,再根据∠BDC=45°,即可解决问题.
②正确.首先证明△DCE≌△EHF,推出CE=FH,在Rt△EDC中,由DE2-DC2=CE2,可得S正方形DEFG-S正方形ABCD=FH2.
③正确.先证明△ADE≌△CDG,推出∠AED=∠DGC,由∠DGO+∠DOG=90°,∠DOG=∠POE,推出∠OEP+∠POE=90°,推出∠OPE=90°.
④错误.由AD∥CE,推出S△ACE=S△DCE,推出$\frac{1}{2}$•AE•CP=$\frac{1}{2}$•CD•CE,推出AE•CP=CD•CE,推出CG•CP=CD•CE,由CD>CE,推出CD•CE<CD2,推出CG•CP<CD2,即可证明.
⑤正确.如图2中,在CD上取一点F,使得DF=EF,连接EF.由∠FDE=∠FED=22.5°,推出∠CFE=∠FDE+∠FED=45°,由∠ECF=90°,推出∠CFE=∠CEF=45°,推出CF=CE,设CF=CE=a,则EF=DF=$\sqrt{2}$a,根据S△CDE:S△BCD=$\frac{1}{2}$•a•(1+$\sqrt{2}$)a:$\frac{1}{2}$[(1+$\sqrt{2}$)a]2计算即可解决问题.
解答 解:如图1中,设CG交DE于O,连接AC.
∵四边形ABCD是正方形,
∴∠DBC=BDC=45°,
∵BD=BE,
∴∠BDE=∠BED=$\frac{180°-45°}{2}$=67.5°,
∴∠CDE=∠BDE-∠BDC=22.5°,故①正确,
∵FH⊥CH,四边形DEFG是正方形,
∴∠DCE=∠EHF=∠DEF=90°,DE=EF,
∴∠DEC+∠FEH=90°,∠FEH+∠EFH=90°,
∴∠DEC=∠EFH,
在△DCE和△EHF中,
$\left\{\begin{array}{l}{∠DCE=∠EHF}\\{∠DEC=∠EFH}\\{DE=EF}\end{array}\right.$,
∴△DCE≌△EHF,
∴CE=FH,
在Rt△EDC中,∵DE2-DC2=CE2,
∴S正方形DEFG-S正方形ABCD=FH2,故②正确,
∵∠ADC=∠GDE=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADE=∠CDG}\\{DE=DG}\end{array}\right.$,
∴△ADE≌△CDG,
∴AE=CG,∠AED=∠DGC,
∵∠DGO+∠DOG=90°,∠DOG=∠POE,
∴∠OEP+∠POE=90°,
∴∠OPE=90°,
∴AE⊥CG,故③正确,
∵AD∥CE,
∴S△ACE=S△DCE,
∴$\frac{1}{2}$•AE•CP=$\frac{1}{2}$•CD•CE,
∴AE•CP=CD•CE,
∴CG•CP=CD•CE,
∵CD>CE,
∴CD•CE<CD2,
∴CG•CP<CD2,故④错误,
如图2中,在CD上取一点F,使得DF=EF,连接EF.
∵∠FDE=∠FED=22.5°,
∴∠CFE=∠FDE+∠FED=45°,∵∠ECF=90°,
∴∠CFE=∠CEF=45°,
∴CF=CE,设CF=CE=a,则EF=DF=$\sqrt{2}$a,
∴S△CDE:S△BCD=$\frac{1}{2}$•a•(1+$\sqrt{2}$)a:$\frac{1}{2}$[(1+$\sqrt{2}$)a]2=$\sqrt{2}$-1,故⑤正确.
故选D.
点评 本题考查正方形的性质、相似三角形的判定和性质、全等三角形的判定和性质、等腰三角形的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会利用面积法解决线段之间的关系问题,学会用转化的思想思考问题,属于中考选择题中的压轴题.

 阅读快车系列答案
阅读快车系列答案| 甲 | 80 | 75 | 90 | 64 | 88 | 95 |
| 乙 | 84 | 80 | 88 | 76 | 79 | 85 |
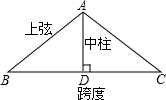 如图,厂房屋顶人字架(等腰三角形)的跨度为20m,∠B=37°,求中柱AD(D为底边中点)和上弦AB的长(参考数据:cos37°≈0.6)
如图,厂房屋顶人字架(等腰三角形)的跨度为20m,∠B=37°,求中柱AD(D为底边中点)和上弦AB的长(参考数据:cos37°≈0.6)